-
PDF
- Split View
-
Views
-
Cite
Cite
Xin Li, Fan Wu, Feng Qi, Daniel A. Beard, A database of thermodynamic properties of the reactions of glycolysis, the tricarboxylic acid cycle, and the pentose phosphate pathway, Database, Volume 2011, 2011, bar005, https://doi.org/10.1093/database/bar005
Close - Share Icon Share
Abstract
A database of thermodynamic properties is developed, which extends a previous database of glycolysis and tricarboxylic acid cycle by adding the reactions of the pentose phosphate pathway. The raw data and documented estimations of solution properties are made electronically available. The database is determined by estimation of a set of parameters representing species-level free energies of formation. The resulting calculations provide thermodynamic and network-based estimates of thermodynamic properties for six reactions of the pentose phosphate pathway for which estimates are not available in the preexisting literature. Optimized results are made available in ThermoML format. Because calculations depend on estimated hydrogen and metal cation dissociation constants, an uncertainty and sensitivity analysis is performed, revealing 23 critical dissociation constants to which the computed thermodynamic properties are particularly sensitive.
Database URL:http://www.biocoda.org/thermo
Introduction
Reliable and self-consistent databases of thermodynamic properties for biochemical reactions are necessary for accurate analysis of biochemical systems (1–6). A recently developed database of thermodynamic properties for the reactions of glycolysis and the tricarboxylic acid cycle that was constituted from measured equilibrium data (7) represents a refinement to the Alberty database (8) in that it accounts for the ionic strength and interactions of biochemical reactants and metal cations (Mg2+, Ca2+, Na+ and K+) in estimating the derived properties from the raw data. The database of Li et al. (7) is a framework that can be extended and refined by adding the underlying raw experimental data in the database and/or refining the underlying model assumptions. Here an updated database is developed by adding the reactions of the pentose phosphate pathway into the original database.
As in Li et al. (7), thermodynamic properties (reference and
) values are estimated by minimizing the difference between model predictions and experimental data. Apparent equilibrium constants for biochemical reactions are estimated by these derived thermodynamic properties and compared to experimental data measured under non-standard conditions. The basic formulae described in Li et al. (7) are used here, which account for temperature, ionic interactions and ion binding (8–13) effects to convert standard-state reference quantities to experimental state quantities.
Input data
Database of measured equilibrium constants
Raw experimental data are obtained from original reports (14–19). As in Li et al. (7), we preferentially select studies rated as A- and B-quality by Goldberg et al. (20–22). Free cation concentrations and ionic strength associated with these original studies are estimated based on the conditions reported in the original sources. All data and calculations are explicitly documented in the database. As we have previously established (7), each measurement entry in the raw-data database provides the following information: (i) enzyme name (EC number); (ii) experimental temperature, pH, ionic strength, apparent equilibrium constant, free metal cation concentrations, buffer and experimental method; (iii) quality rating from Goldberg et al. (20–22); (iv) notes on experiments and strategies of estimations and approximations applied in calculations; and (v) reference information. Up-to-date versions of the experimental database are made available at the URL http://www.biocoda.org/thermo, or by contacting the authors.
Database of reactions and estimated standard reaction enthalpies
There are eight reactions in the pentose phosphate pathway: glucose 6-phosphate dehydrogenase (EC 1.1.1.49, G6PD), 6-phosphogluconolactonase (EC 3.1.1.31, PGL), 6-phosphogluconate dehydrogenase (EC 1.1.1.44, PGD), ribose-5-phosphate isomerase (EC 5.3.1.6, R5PI), ribulose-phosphate 3-epimerase (EC 5.1.3.1, RUPE), transketolase (EC 2.2.1.1, TKL), transaldolase (EC 2.2.1.2, TAL) and transketolase 2 (EC 2.2.1.1, TKL2). The first three reactions are the oxidative pentose phosphate pathway, and the rest are the reductive pentose phosphate pathway (23). After adding these reactions into our original database, there are 33 reactions in total, which are shown in the Table 1 (first 33 reactions). Table 1 lists EC numbers, reaction names and the abbreviations employed, the reference reaction stoichiometries, and estimated standard reaction enthalpies at T = 298.15 K, I = 0 M. In the reference reaction, a superscript is used to indicate the charge of chemical species. For example, the abbreviation for references species for glucose (GLC0) is distinguished from the abbreviation for the biochemical reactant GLC.
| EC No. . | Reaction name . | Reaction abbreviation . | Reference reaction . | |
|---|---|---|---|---|
| EC 2.7.1.1 | Glucokinase | GLK | GLC0 + ATP4− = G6P2− + ADP3− + H+ | −23.8a |
| EC 5.3.1.9 | Phosphoglucose isomerase | PGI | G6P2− = F6P2− | 11.53b |
| EC 2.7.1.11 | Phosphofructokinase | PFK | F6P2− + ATP4− = F16P4− + ADP3− + H+ | −9.5c |
| EC 4.1.2.13 | Fructose-1,6-biphosphatate aldolase | FBA | F16P4− = DHAP2− + GAP2− | 48.97b |
| EC 5.3.1.1 | Triosphosphate isomerase | TPI | GAP2− = DHAP2− | 2.73d |
| EC 4.1.2.13 | Fructose-1,6-biphosphatate aldolase 2 | FBA2 | F16P4− = 2DHAP2− | 51.70b |
| EC 1.2.1.12 | Glyceraldyde-3-P dehydrogenase | GAP | GAP2− + HPO2− 4+ NAD− ox= BPG4− + NAD2− red+ H+ | #e |
| EC 2.7.2.3 | Phosphoglycerate kinase | PGK | GAP2− + HPO2− 4+ NAD− ox+ ADP3− = PG33− + NAD2− red+ ATP4− + H+ | #e |
| EC 5.4.2.1 | Phosphoglycerate mutase | PGYM | PG23− = PG33− | 28.05b |
| EC 4.2.1.11 | Enolase | ENO | PG23− = PEP3− + H2O0 | 15.1b |
| EC 2.7.1.40 | Pyruvate kinase | PYK | PYR− + ATP4− = PEP3− + ADP3− + H+ | 5.415a |
| EC 4.1.3.7 | Citrate synthase | CITS | OAA2− + ACoA0 + H2O0 = CIT3− + COAS− + 2H+ | #e |
| EC 4.2.1.3 | Aconitrate hydratese | ACON | ISCIT3− = CIT3− | −20.0b |
| EC 1.1.1.42 | Isocitrate dehydrogenase | IDH | ISCIT3− + NADP3− ox+ H2O0 = AKG2− + NADP4−red + CO2− 3+ 2H+ | −22.17b |
| EC 6.2.1.4 | Auccinate-CoA ligase | SCS | GTP4- + SUC2− + COAS− + H+ = GDP3− + HPO2−4 + SUCCoA− | −30.9b |
| EC 4.2.1.2 | Fumarate hydratase | FUM | FUM2− + H2O0 = MAL2− | −13.18b |
| EC 1.1.1.37 | Malate dehydrogenase | MDH | MAL2− + NAD− ox= OAA2− + NAD2− red+ H+ | 51.29b |
| EC 2.7.4.6 | Nucleoside-diphosphate kinase | NDK | ATP4− + GDP3− = ADP3− + GTP4− | #e |
| EC 1.6.1.1 | NADP transhydrogenase | NPTH | NAD− ox+ NADP4− red= NAD2− red+ NADP3−ox | −4.1c |
| EC 1.1.1.40 | Malic enzyme | MLE | MAL2− + NADP3− ox+ H2O0 = PYR− + NADP4− red+ CO2- 3+ 2H+ | #e |
| EC 1.1.1.37 | Malate dehydrogenase 2 | MDH2 | MAL2− + ACoA0 + NAD− ox+ H2O0 = CIT3− + COAS− + NAD2− red+ 3H+ | #e |
| EC 2.7.1.23 | NAD+ kinase | NADK | ATP4− + NAD− ox= ADP3− + NADP3− ox+ H+ | #e |
| EC 3.6.1.32 | ATPase | ATPS | ATP4− + H2O0 = ADP3− + HPO2− 4+ H+ | −20.5a |
| EC 3.1.3.1 | Alkaline phosphatase/G6P hydrolysis | G6PH | G6P2− + H2O0 = GLC0 + Pi2− | 0.91a |
| EC 6.4.1.1 | Pyruvate carboxylase | PCL | PYR− + ATP4− + CO2− 3= OAA2− + ADP3− + Pi2− | #e |
| EC 1.1.1.49 | Glucose 6-phosphate dehydrogenase | G6PD | G6P2− + NADP3− ox= PGLT2− + NADP4− red+ H+ | #e |
| EC 3.1.1.31 | 6-Phosphogluconolactonase | PGL | G6P2− + NADP3− ox+ H2O0 = PGN3− + NADP4− red+ 2H+ | #e |
| EC 1.1.1.44 | 6-Phosphogluconate dehydrogenase | PGD | PGN3− + NADP3− ox+ H2O0 = RU5P2− + NADP4−red + CO2− 3+ 2H+ | 37.47b |
| EC 5.3.1.6 | Ribose-5-phosphate isomerase | R5PI | R5P2− = RU5P2− | 12.86b |
| EC 5.1.3.1 | Ribulose-phosphate 3-epimerase | RUPE | RU5P2− = X5P2− | #e |
| EC 2.2.1.1 | Transketolase | TKL | S7P2− + GAP2− = R5P2− + X5P2− | #e |
| EC 2.2.1.2 | Transaldolase | TAL | S7P2− + GAP2− = E4P2− + F6P2− | #e |
| EC 2.2.1.1 | Transketolase 2 | TKL2 | F6P2− + GAP2− = E4P2− + X5P2− | #e |
| EC 1.2.4.1+EC 2.3.1.12+EC 1.8.1.4 | Pyruvate dehydrogenase complex | PDH | PYR− + COAS− + NAD− ox+ H2O = CO2− 3+ ACoA0 + NAD2− red+ H+ | #e |
| EC 1.1.1.41 | Isocitrate dehydrogenase | IDH2 | ISCIT3− + NAD− ox+ H2O0 = AKG2- + NAD2− red+ CO2− 3+ 2H+ | −26.27d |
| EC 1.2.1.52 | α-Ketoglutarate dehydrogenase | AKGDH | AKG2− + NAD−ox + COAS− + H2O0 = SUCCoA− + NAD2− red+ CO2- 3+ H+ | #e |
| EC 1.3.5.1 | Succinate dehydrogenase | SDH | SUC2− + CoQ0 = FUM2− + CoQH02 | #e |
| EC No. . | Reaction name . | Reaction abbreviation . | Reference reaction . | |
|---|---|---|---|---|
| EC 2.7.1.1 | Glucokinase | GLK | GLC0 + ATP4− = G6P2− + ADP3− + H+ | −23.8a |
| EC 5.3.1.9 | Phosphoglucose isomerase | PGI | G6P2− = F6P2− | 11.53b |
| EC 2.7.1.11 | Phosphofructokinase | PFK | F6P2− + ATP4− = F16P4− + ADP3− + H+ | −9.5c |
| EC 4.1.2.13 | Fructose-1,6-biphosphatate aldolase | FBA | F16P4− = DHAP2− + GAP2− | 48.97b |
| EC 5.3.1.1 | Triosphosphate isomerase | TPI | GAP2− = DHAP2− | 2.73d |
| EC 4.1.2.13 | Fructose-1,6-biphosphatate aldolase 2 | FBA2 | F16P4− = 2DHAP2− | 51.70b |
| EC 1.2.1.12 | Glyceraldyde-3-P dehydrogenase | GAP | GAP2− + HPO2− 4+ NAD− ox= BPG4− + NAD2− red+ H+ | #e |
| EC 2.7.2.3 | Phosphoglycerate kinase | PGK | GAP2− + HPO2− 4+ NAD− ox+ ADP3− = PG33− + NAD2− red+ ATP4− + H+ | #e |
| EC 5.4.2.1 | Phosphoglycerate mutase | PGYM | PG23− = PG33− | 28.05b |
| EC 4.2.1.11 | Enolase | ENO | PG23− = PEP3− + H2O0 | 15.1b |
| EC 2.7.1.40 | Pyruvate kinase | PYK | PYR− + ATP4− = PEP3− + ADP3− + H+ | 5.415a |
| EC 4.1.3.7 | Citrate synthase | CITS | OAA2− + ACoA0 + H2O0 = CIT3− + COAS− + 2H+ | #e |
| EC 4.2.1.3 | Aconitrate hydratese | ACON | ISCIT3− = CIT3− | −20.0b |
| EC 1.1.1.42 | Isocitrate dehydrogenase | IDH | ISCIT3− + NADP3− ox+ H2O0 = AKG2− + NADP4−red + CO2− 3+ 2H+ | −22.17b |
| EC 6.2.1.4 | Auccinate-CoA ligase | SCS | GTP4- + SUC2− + COAS− + H+ = GDP3− + HPO2−4 + SUCCoA− | −30.9b |
| EC 4.2.1.2 | Fumarate hydratase | FUM | FUM2− + H2O0 = MAL2− | −13.18b |
| EC 1.1.1.37 | Malate dehydrogenase | MDH | MAL2− + NAD− ox= OAA2− + NAD2− red+ H+ | 51.29b |
| EC 2.7.4.6 | Nucleoside-diphosphate kinase | NDK | ATP4− + GDP3− = ADP3− + GTP4− | #e |
| EC 1.6.1.1 | NADP transhydrogenase | NPTH | NAD− ox+ NADP4− red= NAD2− red+ NADP3−ox | −4.1c |
| EC 1.1.1.40 | Malic enzyme | MLE | MAL2− + NADP3− ox+ H2O0 = PYR− + NADP4− red+ CO2- 3+ 2H+ | #e |
| EC 1.1.1.37 | Malate dehydrogenase 2 | MDH2 | MAL2− + ACoA0 + NAD− ox+ H2O0 = CIT3− + COAS− + NAD2− red+ 3H+ | #e |
| EC 2.7.1.23 | NAD+ kinase | NADK | ATP4− + NAD− ox= ADP3− + NADP3− ox+ H+ | #e |
| EC 3.6.1.32 | ATPase | ATPS | ATP4− + H2O0 = ADP3− + HPO2− 4+ H+ | −20.5a |
| EC 3.1.3.1 | Alkaline phosphatase/G6P hydrolysis | G6PH | G6P2− + H2O0 = GLC0 + Pi2− | 0.91a |
| EC 6.4.1.1 | Pyruvate carboxylase | PCL | PYR− + ATP4− + CO2− 3= OAA2− + ADP3− + Pi2− | #e |
| EC 1.1.1.49 | Glucose 6-phosphate dehydrogenase | G6PD | G6P2− + NADP3− ox= PGLT2− + NADP4− red+ H+ | #e |
| EC 3.1.1.31 | 6-Phosphogluconolactonase | PGL | G6P2− + NADP3− ox+ H2O0 = PGN3− + NADP4− red+ 2H+ | #e |
| EC 1.1.1.44 | 6-Phosphogluconate dehydrogenase | PGD | PGN3− + NADP3− ox+ H2O0 = RU5P2− + NADP4−red + CO2− 3+ 2H+ | 37.47b |
| EC 5.3.1.6 | Ribose-5-phosphate isomerase | R5PI | R5P2− = RU5P2− | 12.86b |
| EC 5.1.3.1 | Ribulose-phosphate 3-epimerase | RUPE | RU5P2− = X5P2− | #e |
| EC 2.2.1.1 | Transketolase | TKL | S7P2− + GAP2− = R5P2− + X5P2− | #e |
| EC 2.2.1.2 | Transaldolase | TAL | S7P2− + GAP2− = E4P2− + F6P2− | #e |
| EC 2.2.1.1 | Transketolase 2 | TKL2 | F6P2− + GAP2− = E4P2− + X5P2− | #e |
| EC 1.2.4.1+EC 2.3.1.12+EC 1.8.1.4 | Pyruvate dehydrogenase complex | PDH | PYR− + COAS− + NAD− ox+ H2O = CO2− 3+ ACoA0 + NAD2− red+ H+ | #e |
| EC 1.1.1.41 | Isocitrate dehydrogenase | IDH2 | ISCIT3− + NAD− ox+ H2O0 = AKG2- + NAD2− red+ CO2− 3+ 2H+ | −26.27d |
| EC 1.2.1.52 | α-Ketoglutarate dehydrogenase | AKGDH | AKG2− + NAD−ox + COAS− + H2O0 = SUCCoA− + NAD2− red+ CO2- 3+ H+ | #e |
| EC 1.3.5.1 | Succinate dehydrogenase | SDH | SUC2− + CoQ0 = FUM2− + CoQH02 | #e |
| EC No. . | Reaction name . | Reaction abbreviation . | Reference reaction . | |
|---|---|---|---|---|
| EC 2.7.1.1 | Glucokinase | GLK | GLC0 + ATP4− = G6P2− + ADP3− + H+ | −23.8a |
| EC 5.3.1.9 | Phosphoglucose isomerase | PGI | G6P2− = F6P2− | 11.53b |
| EC 2.7.1.11 | Phosphofructokinase | PFK | F6P2− + ATP4− = F16P4− + ADP3− + H+ | −9.5c |
| EC 4.1.2.13 | Fructose-1,6-biphosphatate aldolase | FBA | F16P4− = DHAP2− + GAP2− | 48.97b |
| EC 5.3.1.1 | Triosphosphate isomerase | TPI | GAP2− = DHAP2− | 2.73d |
| EC 4.1.2.13 | Fructose-1,6-biphosphatate aldolase 2 | FBA2 | F16P4− = 2DHAP2− | 51.70b |
| EC 1.2.1.12 | Glyceraldyde-3-P dehydrogenase | GAP | GAP2− + HPO2− 4+ NAD− ox= BPG4− + NAD2− red+ H+ | #e |
| EC 2.7.2.3 | Phosphoglycerate kinase | PGK | GAP2− + HPO2− 4+ NAD− ox+ ADP3− = PG33− + NAD2− red+ ATP4− + H+ | #e |
| EC 5.4.2.1 | Phosphoglycerate mutase | PGYM | PG23− = PG33− | 28.05b |
| EC 4.2.1.11 | Enolase | ENO | PG23− = PEP3− + H2O0 | 15.1b |
| EC 2.7.1.40 | Pyruvate kinase | PYK | PYR− + ATP4− = PEP3− + ADP3− + H+ | 5.415a |
| EC 4.1.3.7 | Citrate synthase | CITS | OAA2− + ACoA0 + H2O0 = CIT3− + COAS− + 2H+ | #e |
| EC 4.2.1.3 | Aconitrate hydratese | ACON | ISCIT3− = CIT3− | −20.0b |
| EC 1.1.1.42 | Isocitrate dehydrogenase | IDH | ISCIT3− + NADP3− ox+ H2O0 = AKG2− + NADP4−red + CO2− 3+ 2H+ | −22.17b |
| EC 6.2.1.4 | Auccinate-CoA ligase | SCS | GTP4- + SUC2− + COAS− + H+ = GDP3− + HPO2−4 + SUCCoA− | −30.9b |
| EC 4.2.1.2 | Fumarate hydratase | FUM | FUM2− + H2O0 = MAL2− | −13.18b |
| EC 1.1.1.37 | Malate dehydrogenase | MDH | MAL2− + NAD− ox= OAA2− + NAD2− red+ H+ | 51.29b |
| EC 2.7.4.6 | Nucleoside-diphosphate kinase | NDK | ATP4− + GDP3− = ADP3− + GTP4− | #e |
| EC 1.6.1.1 | NADP transhydrogenase | NPTH | NAD− ox+ NADP4− red= NAD2− red+ NADP3−ox | −4.1c |
| EC 1.1.1.40 | Malic enzyme | MLE | MAL2− + NADP3− ox+ H2O0 = PYR− + NADP4− red+ CO2- 3+ 2H+ | #e |
| EC 1.1.1.37 | Malate dehydrogenase 2 | MDH2 | MAL2− + ACoA0 + NAD− ox+ H2O0 = CIT3− + COAS− + NAD2− red+ 3H+ | #e |
| EC 2.7.1.23 | NAD+ kinase | NADK | ATP4− + NAD− ox= ADP3− + NADP3− ox+ H+ | #e |
| EC 3.6.1.32 | ATPase | ATPS | ATP4− + H2O0 = ADP3− + HPO2− 4+ H+ | −20.5a |
| EC 3.1.3.1 | Alkaline phosphatase/G6P hydrolysis | G6PH | G6P2− + H2O0 = GLC0 + Pi2− | 0.91a |
| EC 6.4.1.1 | Pyruvate carboxylase | PCL | PYR− + ATP4− + CO2− 3= OAA2− + ADP3− + Pi2− | #e |
| EC 1.1.1.49 | Glucose 6-phosphate dehydrogenase | G6PD | G6P2− + NADP3− ox= PGLT2− + NADP4− red+ H+ | #e |
| EC 3.1.1.31 | 6-Phosphogluconolactonase | PGL | G6P2− + NADP3− ox+ H2O0 = PGN3− + NADP4− red+ 2H+ | #e |
| EC 1.1.1.44 | 6-Phosphogluconate dehydrogenase | PGD | PGN3− + NADP3− ox+ H2O0 = RU5P2− + NADP4−red + CO2− 3+ 2H+ | 37.47b |
| EC 5.3.1.6 | Ribose-5-phosphate isomerase | R5PI | R5P2− = RU5P2− | 12.86b |
| EC 5.1.3.1 | Ribulose-phosphate 3-epimerase | RUPE | RU5P2− = X5P2− | #e |
| EC 2.2.1.1 | Transketolase | TKL | S7P2− + GAP2− = R5P2− + X5P2− | #e |
| EC 2.2.1.2 | Transaldolase | TAL | S7P2− + GAP2− = E4P2− + F6P2− | #e |
| EC 2.2.1.1 | Transketolase 2 | TKL2 | F6P2− + GAP2− = E4P2− + X5P2− | #e |
| EC 1.2.4.1+EC 2.3.1.12+EC 1.8.1.4 | Pyruvate dehydrogenase complex | PDH | PYR− + COAS− + NAD− ox+ H2O = CO2− 3+ ACoA0 + NAD2− red+ H+ | #e |
| EC 1.1.1.41 | Isocitrate dehydrogenase | IDH2 | ISCIT3− + NAD− ox+ H2O0 = AKG2- + NAD2− red+ CO2− 3+ 2H+ | −26.27d |
| EC 1.2.1.52 | α-Ketoglutarate dehydrogenase | AKGDH | AKG2− + NAD−ox + COAS− + H2O0 = SUCCoA− + NAD2− red+ CO2- 3+ H+ | #e |
| EC 1.3.5.1 | Succinate dehydrogenase | SDH | SUC2− + CoQ0 = FUM2− + CoQH02 | #e |
| EC No. . | Reaction name . | Reaction abbreviation . | Reference reaction . | |
|---|---|---|---|---|
| EC 2.7.1.1 | Glucokinase | GLK | GLC0 + ATP4− = G6P2− + ADP3− + H+ | −23.8a |
| EC 5.3.1.9 | Phosphoglucose isomerase | PGI | G6P2− = F6P2− | 11.53b |
| EC 2.7.1.11 | Phosphofructokinase | PFK | F6P2− + ATP4− = F16P4− + ADP3− + H+ | −9.5c |
| EC 4.1.2.13 | Fructose-1,6-biphosphatate aldolase | FBA | F16P4− = DHAP2− + GAP2− | 48.97b |
| EC 5.3.1.1 | Triosphosphate isomerase | TPI | GAP2− = DHAP2− | 2.73d |
| EC 4.1.2.13 | Fructose-1,6-biphosphatate aldolase 2 | FBA2 | F16P4− = 2DHAP2− | 51.70b |
| EC 1.2.1.12 | Glyceraldyde-3-P dehydrogenase | GAP | GAP2− + HPO2− 4+ NAD− ox= BPG4− + NAD2− red+ H+ | #e |
| EC 2.7.2.3 | Phosphoglycerate kinase | PGK | GAP2− + HPO2− 4+ NAD− ox+ ADP3− = PG33− + NAD2− red+ ATP4− + H+ | #e |
| EC 5.4.2.1 | Phosphoglycerate mutase | PGYM | PG23− = PG33− | 28.05b |
| EC 4.2.1.11 | Enolase | ENO | PG23− = PEP3− + H2O0 | 15.1b |
| EC 2.7.1.40 | Pyruvate kinase | PYK | PYR− + ATP4− = PEP3− + ADP3− + H+ | 5.415a |
| EC 4.1.3.7 | Citrate synthase | CITS | OAA2− + ACoA0 + H2O0 = CIT3− + COAS− + 2H+ | #e |
| EC 4.2.1.3 | Aconitrate hydratese | ACON | ISCIT3− = CIT3− | −20.0b |
| EC 1.1.1.42 | Isocitrate dehydrogenase | IDH | ISCIT3− + NADP3− ox+ H2O0 = AKG2− + NADP4−red + CO2− 3+ 2H+ | −22.17b |
| EC 6.2.1.4 | Auccinate-CoA ligase | SCS | GTP4- + SUC2− + COAS− + H+ = GDP3− + HPO2−4 + SUCCoA− | −30.9b |
| EC 4.2.1.2 | Fumarate hydratase | FUM | FUM2− + H2O0 = MAL2− | −13.18b |
| EC 1.1.1.37 | Malate dehydrogenase | MDH | MAL2− + NAD− ox= OAA2− + NAD2− red+ H+ | 51.29b |
| EC 2.7.4.6 | Nucleoside-diphosphate kinase | NDK | ATP4− + GDP3− = ADP3− + GTP4− | #e |
| EC 1.6.1.1 | NADP transhydrogenase | NPTH | NAD− ox+ NADP4− red= NAD2− red+ NADP3−ox | −4.1c |
| EC 1.1.1.40 | Malic enzyme | MLE | MAL2− + NADP3− ox+ H2O0 = PYR− + NADP4− red+ CO2- 3+ 2H+ | #e |
| EC 1.1.1.37 | Malate dehydrogenase 2 | MDH2 | MAL2− + ACoA0 + NAD− ox+ H2O0 = CIT3− + COAS− + NAD2− red+ 3H+ | #e |
| EC 2.7.1.23 | NAD+ kinase | NADK | ATP4− + NAD− ox= ADP3− + NADP3− ox+ H+ | #e |
| EC 3.6.1.32 | ATPase | ATPS | ATP4− + H2O0 = ADP3− + HPO2− 4+ H+ | −20.5a |
| EC 3.1.3.1 | Alkaline phosphatase/G6P hydrolysis | G6PH | G6P2− + H2O0 = GLC0 + Pi2− | 0.91a |
| EC 6.4.1.1 | Pyruvate carboxylase | PCL | PYR− + ATP4− + CO2− 3= OAA2− + ADP3− + Pi2− | #e |
| EC 1.1.1.49 | Glucose 6-phosphate dehydrogenase | G6PD | G6P2− + NADP3− ox= PGLT2− + NADP4− red+ H+ | #e |
| EC 3.1.1.31 | 6-Phosphogluconolactonase | PGL | G6P2− + NADP3− ox+ H2O0 = PGN3− + NADP4− red+ 2H+ | #e |
| EC 1.1.1.44 | 6-Phosphogluconate dehydrogenase | PGD | PGN3− + NADP3− ox+ H2O0 = RU5P2− + NADP4−red + CO2− 3+ 2H+ | 37.47b |
| EC 5.3.1.6 | Ribose-5-phosphate isomerase | R5PI | R5P2− = RU5P2− | 12.86b |
| EC 5.1.3.1 | Ribulose-phosphate 3-epimerase | RUPE | RU5P2− = X5P2− | #e |
| EC 2.2.1.1 | Transketolase | TKL | S7P2− + GAP2− = R5P2− + X5P2− | #e |
| EC 2.2.1.2 | Transaldolase | TAL | S7P2− + GAP2− = E4P2− + F6P2− | #e |
| EC 2.2.1.1 | Transketolase 2 | TKL2 | F6P2− + GAP2− = E4P2− + X5P2− | #e |
| EC 1.2.4.1+EC 2.3.1.12+EC 1.8.1.4 | Pyruvate dehydrogenase complex | PDH | PYR− + COAS− + NAD− ox+ H2O = CO2− 3+ ACoA0 + NAD2− red+ H+ | #e |
| EC 1.1.1.41 | Isocitrate dehydrogenase | IDH2 | ISCIT3− + NAD− ox+ H2O0 = AKG2- + NAD2− red+ CO2− 3+ 2H+ | −26.27d |
| EC 1.2.1.52 | α-Ketoglutarate dehydrogenase | AKGDH | AKG2− + NAD−ox + COAS− + H2O0 = SUCCoA− + NAD2− red+ CO2- 3+ H+ | #e |
| EC 1.3.5.1 | Succinate dehydrogenase | SDH | SUC2− + CoQ0 = FUM2− + CoQH02 | #e |
Reaction enthalpies () for two reactions in the pentose phosphate pathway (PGD and R5PI) can be estimated using van't Hoff equation because data on apparent equilibrium constants at different temperatures are available. Neither equilibrium data at different temperatures nor prior values of
are available for the other six reactions of the pentose phosphate pathway; hence the symbol ‘#’ is used to denote the absence of data. For these cases, the value is set to zero in further calculations.
Database of reactant and dissociation constants
There are seven reactants introduced to the reactant database by adding the pentose phosphate pathway into the thermodynamic database: erythrose 4-phosphate (E4P), 6-phosphoglucono-δ-lactone (PGLT), 6-phospho-d-gluconate (PGN), ribose 5-phosphate (R5P), ribulose 5-phosphate (RU5P), sedoheptulose 7-phosphate (S7P) and xylulose 5-phosphate (X5P). For the five sugar phosphates (E4P, R5P, RU5P, S7P and X5P), cation dissociation constants for only R5P can be found in NIST database. Since E4P, RU5P, S7P and X5P are structurally similar substances to R5P (all have similar near neighbors to the phosphate group), a pragmatic approach to estimate the necessary dissociation constants is to use the values for R5P (24). Specifically, E4P, RU5P, S7P and X5P are assumed to have dissociation properties equal to those for R5P in our calculations. For PGLT, we use the pKH1 value of 5.99 from Alberty (10). For PGN, Casazza et al. (15) report that the hydrogen ion dissociation constant for the carboxylic acid is >1.0E-4, while the constant for the phosphate ester is the same as that of glucose 6-P [pKH1 = 5.99 (10)]. Here we arbitrarily assign the value of 4.995 to the pKH1 for PGN, which is the average of 4 and 5.99. The uncertainties of these assignments are considered in the uncertainty and sensitivity analysis below.
Basic thermodynamic and ion binding data for biochemical reactants and associated reference species are listed in Table 2. Each entry in the table contains the following information: (i) detailed name of reactant; (ii) reference species abbreviation; (iii) reactant abbreviation; (iv) number of protons in reference species; and (v) the dissociation constants (provided as pK) and the corresponding dissociation enthalpies Dissociation constants and enthalpies are tabulated at 298.15 K and 0.1 M ionic strength. The symbol ‘#’ is used to indicate absence of data. For these cases, the pK's are assumed to be infinite (no binding) with corresponding dissociation constants equal to zero. In the calculations, all the pK and
values are adjusted to a common reference state of T = 298.15 K and I = 0.
| Reactant . | Reference species abbreviationb . | Reactant abbreviation . | NHb . | pKH1 . | pKH2 . | pKMg1 . | pKHMg . | pKMg2 . | pKK1 . | pKNa1 . | pKHNa . | pKCa1 . | pKHCa . | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Acetyl-coenzyme A | ACoA0 | ACoA | 3 | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Adenosine diphosphate | ADP3− | ADP | 12 | 6.496 | −2 | 3.87 | 16 | 3.3 | −15 | 1.59 | −7.5 | 1.27 | −11.76 | 1 | # | 1.12 | # | # | # | 2.86 | −9.6 | 1.48 | −6.2 |
| Adenosine triphosphate | ATP4− | ATP | 12 | 6.71 | −2 | 3.99 | 15 | 4.28 | −18 | 2.32 | −9.6 | 1.7 | −17.52 | 1.17 | −1 | 1.31 | 0.8 | # | # | 3.95 | −13 | 2.16 | −7.9 |
| 1,3-Bisphosphoglycerate | BPG4− | BPG | 4 | 7.1c | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Citrate | CIT3− | CIT | 5 | 5.67 | −1.9 | 4.35 | 3.1 | 3.517 | −8 | 1.8 | # | # | # | 0.6 | −3.54 | 0.75 | −1 | # | # | 3.54 | −1.2 | 2.07 | # |
| Coenzyme A-SH | COAS− | COAS | 0 | 8.17c | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Carbon dioxide (total) | CO2−3 | CO2_tot | 0 | 9.9c | 16.1c | 6.15c | 8.27c | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Dihydroxyacetone phosphate | DHAP2− | DHAP | 5 | 5.9 | # | # | # | 1.57 | # | # | # | # | # | # | # | # | # | # | # | 1.38 | # | # | # |
| d-fructose 6-phosphate | F6P2− | F6P | 11 | 5.89 | −0.559d | 1.1 | # | 1.74e | −9.72d | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| d-fructose 1,6-phosphate | F16P4− | F16P | 10 | 6.64 | # | 5.92 | # | 2.7 | # | 2.12 | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Fumarate | FUM2− | FUM | 2 | 4.09 | −1.56 | 2.86 | 1.08 | # | # | # | # | # | # | # | # | # | # | # | # | 0.6 | −6.44 | # | # |
| d-glucose 6-phosphate | G6P2− | G6P | 11 | 5.89e | −0.559d | # | # | 1.74b | −9.72d | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| d-glyceraldehyde 3-phosphate | GAP2− | GAP | 5 | 5.27c | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Guanosine diphosphate | GDP3− | GDP | 12 | 6.505 | −2.14 | 2.8 | # | 3.4 | −7.1 | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| d-glucose | GLC0 | GLC | 12 | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Guanosine triphosphate | GTP4− | GTP | 12 | 6.63 | −3 | 2.93 | 7.1 | 4.31 | −17 | 2.31 | # | # | # | # | # | # | # | # | # | 3.7 | # | # | # |
| Water | H2O0 | H2O | 2 | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Isocitrate | ISCIT3− | ISCIT | 5 | 5.765 | # | 4.29 | # | 2.625 | # | 1.43 | # | # | # | # | # | # | # | # | # | 2.54 | # | # | # |
| α-Ketoglutarate | AKG2− | AKG | 4 | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Malate | MAL2− | MAL | 4 | 4.715 | −0.58 | 3.265 | 3.4 | 1.71 | −6.16 | 0.9f | # | # | # | 0.18 | −2.86 | 0.28 | 0.4 | # | # | 2.005 | −1.06 | 1.06 | 8 |
| NADox | NAD−ox | NADox | 26 | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| NADred | NAD2−red | NADred | 27 | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| NADPox | NADP3−ox | NADPox | 25 | 6.255k | # | 3.874k | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| NADPred | NADP4−red | NADPred | 26 | 6.255l | # | 3.874l | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Oxaloacetate | OAA2− | OAA | 2 | 3.9 | 5.24 | 2.26 | 16.62 | 1.02 | # | # | # | # | # | # | # | # | # | # | # | 1.6 | # | # | # |
| Orthophosphate | HPO2−4 | Pi | 1 | 6.78 | 4.6 | 1.945 | −8.7 | 1.823 | −9.518 | 0.669 | # | # | # | 0.5 | # | 0.61 | # | 0.0856 | # | 1.745 | −9.518 | 0.921 | −10.759 |
| 2-Phospho-d-glycerate | PG23− | PG2 | 4 | 7 | # | 3.55 | # | 2.45 | # | # | # | # | # | 1.18 | # | # | # | # | # | # | # | # | # |
| 3-Phospho-d-glycerate | PG33− | PG3 | 4 | 6.89c | # | 3.64g | # | 2.21h | # | # | # | # | # | 0.87 h | # | # | # | # | # | # | # | # | # |
| Phosphoenolpyruvate | PEP3− | PEP | 2 | 6.245 | # | 3.45 | # | 2.26 | # | # | # | # | # | 1.08 | # | # | # | # | # | # | # | # | # |
| Pyruvate | PYR− | PYR | 3 | 2.26 | 12.8 | # | # | 1.1 | # | # | # | # | # | # | # | # | # | # | # | 0.8 | # | # | # |
| Succinate | SUC2− | SUC | 4 | 5.275 | 0.41 | 4.02 | 3 | 1.355 | # | 0.62 | # | # | # | 0.43 | −2.76 | 0.4212 | −2.759 | # | # | 1.405 | −8.939 | 0.65 | −8 |
| Succinyl-CoA | SUCCoA− | SUCCoA | 4 | 3.99c | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Erythrose 4-phosphate | E4P2− | E4P | 9 | 6.255i | −9.75i | 2i | # | 1.58i | −9.71i | # | # | # | # | # | # | # | # | # | # | 1.48i | # | # | # |
| 6-Phosphoglucono-δ-lactone | PGLT2− | PGLT | 11 | 5.99c | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| 6-Phosphogluconate | PGN3− | PGN | 13 | 4.995j | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Ribose 5-phosphate | R5P2− | R5P | 11 | 6.255 | −9.75 | 2 | # | 1.58 | −9.71d | # | # | # | # | # | # | # | # | # | # | 1.48 | # | # | # |
| Ribulose 5-phosphate | RU5P2− | RU5P | 11 | 6.255i | −9.75i | 2i | # | 1.58i | −9.71i | # | # | # | # | # | # | # | # | # | # | 1.48i | # | # | # |
| Sedoheptulose 7-phosphate | S7P2− | S7P | 15 | 6.255i | −9.75i | 2i | # | 1.58i | −9.71i | # | # | # | # | # | # | # | # | # | # | 1.48i | # | # | # |
| Xylulose 5-phosphate | X5P2− | X5P | 11 | 6.255i | −9.75i | 2i | # | 1.58i | −9.71i | # | # | # | # | # | # | # | # | # | # | 1.48i | # | # | # |
| Reactant . | Reference species abbreviationb . | Reactant abbreviation . | NHb . | pKH1 . | pKH2 . | pKMg1 . | pKHMg . | pKMg2 . | pKK1 . | pKNa1 . | pKHNa . | pKCa1 . | pKHCa . | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Acetyl-coenzyme A | ACoA0 | ACoA | 3 | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Adenosine diphosphate | ADP3− | ADP | 12 | 6.496 | −2 | 3.87 | 16 | 3.3 | −15 | 1.59 | −7.5 | 1.27 | −11.76 | 1 | # | 1.12 | # | # | # | 2.86 | −9.6 | 1.48 | −6.2 |
| Adenosine triphosphate | ATP4− | ATP | 12 | 6.71 | −2 | 3.99 | 15 | 4.28 | −18 | 2.32 | −9.6 | 1.7 | −17.52 | 1.17 | −1 | 1.31 | 0.8 | # | # | 3.95 | −13 | 2.16 | −7.9 |
| 1,3-Bisphosphoglycerate | BPG4− | BPG | 4 | 7.1c | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Citrate | CIT3− | CIT | 5 | 5.67 | −1.9 | 4.35 | 3.1 | 3.517 | −8 | 1.8 | # | # | # | 0.6 | −3.54 | 0.75 | −1 | # | # | 3.54 | −1.2 | 2.07 | # |
| Coenzyme A-SH | COAS− | COAS | 0 | 8.17c | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Carbon dioxide (total) | CO2−3 | CO2_tot | 0 | 9.9c | 16.1c | 6.15c | 8.27c | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Dihydroxyacetone phosphate | DHAP2− | DHAP | 5 | 5.9 | # | # | # | 1.57 | # | # | # | # | # | # | # | # | # | # | # | 1.38 | # | # | # |
| d-fructose 6-phosphate | F6P2− | F6P | 11 | 5.89 | −0.559d | 1.1 | # | 1.74e | −9.72d | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| d-fructose 1,6-phosphate | F16P4− | F16P | 10 | 6.64 | # | 5.92 | # | 2.7 | # | 2.12 | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Fumarate | FUM2− | FUM | 2 | 4.09 | −1.56 | 2.86 | 1.08 | # | # | # | # | # | # | # | # | # | # | # | # | 0.6 | −6.44 | # | # |
| d-glucose 6-phosphate | G6P2− | G6P | 11 | 5.89e | −0.559d | # | # | 1.74b | −9.72d | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| d-glyceraldehyde 3-phosphate | GAP2− | GAP | 5 | 5.27c | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Guanosine diphosphate | GDP3− | GDP | 12 | 6.505 | −2.14 | 2.8 | # | 3.4 | −7.1 | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| d-glucose | GLC0 | GLC | 12 | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Guanosine triphosphate | GTP4− | GTP | 12 | 6.63 | −3 | 2.93 | 7.1 | 4.31 | −17 | 2.31 | # | # | # | # | # | # | # | # | # | 3.7 | # | # | # |
| Water | H2O0 | H2O | 2 | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Isocitrate | ISCIT3− | ISCIT | 5 | 5.765 | # | 4.29 | # | 2.625 | # | 1.43 | # | # | # | # | # | # | # | # | # | 2.54 | # | # | # |
| α-Ketoglutarate | AKG2− | AKG | 4 | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Malate | MAL2− | MAL | 4 | 4.715 | −0.58 | 3.265 | 3.4 | 1.71 | −6.16 | 0.9f | # | # | # | 0.18 | −2.86 | 0.28 | 0.4 | # | # | 2.005 | −1.06 | 1.06 | 8 |
| NADox | NAD−ox | NADox | 26 | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| NADred | NAD2−red | NADred | 27 | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| NADPox | NADP3−ox | NADPox | 25 | 6.255k | # | 3.874k | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| NADPred | NADP4−red | NADPred | 26 | 6.255l | # | 3.874l | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Oxaloacetate | OAA2− | OAA | 2 | 3.9 | 5.24 | 2.26 | 16.62 | 1.02 | # | # | # | # | # | # | # | # | # | # | # | 1.6 | # | # | # |
| Orthophosphate | HPO2−4 | Pi | 1 | 6.78 | 4.6 | 1.945 | −8.7 | 1.823 | −9.518 | 0.669 | # | # | # | 0.5 | # | 0.61 | # | 0.0856 | # | 1.745 | −9.518 | 0.921 | −10.759 |
| 2-Phospho-d-glycerate | PG23− | PG2 | 4 | 7 | # | 3.55 | # | 2.45 | # | # | # | # | # | 1.18 | # | # | # | # | # | # | # | # | # |
| 3-Phospho-d-glycerate | PG33− | PG3 | 4 | 6.89c | # | 3.64g | # | 2.21h | # | # | # | # | # | 0.87 h | # | # | # | # | # | # | # | # | # |
| Phosphoenolpyruvate | PEP3− | PEP | 2 | 6.245 | # | 3.45 | # | 2.26 | # | # | # | # | # | 1.08 | # | # | # | # | # | # | # | # | # |
| Pyruvate | PYR− | PYR | 3 | 2.26 | 12.8 | # | # | 1.1 | # | # | # | # | # | # | # | # | # | # | # | 0.8 | # | # | # |
| Succinate | SUC2− | SUC | 4 | 5.275 | 0.41 | 4.02 | 3 | 1.355 | # | 0.62 | # | # | # | 0.43 | −2.76 | 0.4212 | −2.759 | # | # | 1.405 | −8.939 | 0.65 | −8 |
| Succinyl-CoA | SUCCoA− | SUCCoA | 4 | 3.99c | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Erythrose 4-phosphate | E4P2− | E4P | 9 | 6.255i | −9.75i | 2i | # | 1.58i | −9.71i | # | # | # | # | # | # | # | # | # | # | 1.48i | # | # | # |
| 6-Phosphoglucono-δ-lactone | PGLT2− | PGLT | 11 | 5.99c | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| 6-Phosphogluconate | PGN3− | PGN | 13 | 4.995j | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Ribose 5-phosphate | R5P2− | R5P | 11 | 6.255 | −9.75 | 2 | # | 1.58 | −9.71d | # | # | # | # | # | # | # | # | # | # | 1.48 | # | # | # |
| Ribulose 5-phosphate | RU5P2− | RU5P | 11 | 6.255i | −9.75i | 2i | # | 1.58i | −9.71i | # | # | # | # | # | # | # | # | # | # | 1.48i | # | # | # |
| Sedoheptulose 7-phosphate | S7P2− | S7P | 15 | 6.255i | −9.75i | 2i | # | 1.58i | −9.71i | # | # | # | # | # | # | # | # | # | # | 1.48i | # | # | # |
| Xylulose 5-phosphate | X5P2− | X5P | 11 | 6.255i | −9.75i | 2i | # | 1.58i | −9.71i | # | # | # | # | # | # | # | # | # | # | 1.48i | # | # | # |
aDissociation pK and are reported for T = 298.15 K and I = 0.1 M. Unless indicated, values are the average number obtained from NIST database (27). Dissociation enthalpies are reported in units of kJ/mol. Subscripts on ‘pK’ and ‘
’ entries are defined as follows: ‘H’: hydrogen, ‘Mg’: magnesium, ‘K’: potassium, ‘Na’: sodium, ‘Ca’: calcium, ‘1’: first ion dissociation, ‘2’: second ion dissociation, ‘HMg’: hydrogen ion binds to the ligand before magnesium ion binds to the ligand. ‘#’ denotes value is not available.
bAlberty (8).
dTewari et al. (35).
eG6P and F6P are assumed to have equivalent H+ and Mg2+-dissociation properties.
fFrom NIST database (36) at T = 293.15 K.
gLarsson-Raźnikiewicz (37).
hMerrill et al. (38).
iE4P, RU5P, S7P and X5P are assumed to have equivalent dissociation properties as R5P (24).
jCasazza et al. (15).
kBriggs et al. (39).
lNADPred is assumed to have equivalent dissociation properties as NADPox.
| Reactant . | Reference species abbreviationb . | Reactant abbreviation . | NHb . | pKH1 . | pKH2 . | pKMg1 . | pKHMg . | pKMg2 . | pKK1 . | pKNa1 . | pKHNa . | pKCa1 . | pKHCa . | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Acetyl-coenzyme A | ACoA0 | ACoA | 3 | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Adenosine diphosphate | ADP3− | ADP | 12 | 6.496 | −2 | 3.87 | 16 | 3.3 | −15 | 1.59 | −7.5 | 1.27 | −11.76 | 1 | # | 1.12 | # | # | # | 2.86 | −9.6 | 1.48 | −6.2 |
| Adenosine triphosphate | ATP4− | ATP | 12 | 6.71 | −2 | 3.99 | 15 | 4.28 | −18 | 2.32 | −9.6 | 1.7 | −17.52 | 1.17 | −1 | 1.31 | 0.8 | # | # | 3.95 | −13 | 2.16 | −7.9 |
| 1,3-Bisphosphoglycerate | BPG4− | BPG | 4 | 7.1c | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Citrate | CIT3− | CIT | 5 | 5.67 | −1.9 | 4.35 | 3.1 | 3.517 | −8 | 1.8 | # | # | # | 0.6 | −3.54 | 0.75 | −1 | # | # | 3.54 | −1.2 | 2.07 | # |
| Coenzyme A-SH | COAS− | COAS | 0 | 8.17c | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Carbon dioxide (total) | CO2−3 | CO2_tot | 0 | 9.9c | 16.1c | 6.15c | 8.27c | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Dihydroxyacetone phosphate | DHAP2− | DHAP | 5 | 5.9 | # | # | # | 1.57 | # | # | # | # | # | # | # | # | # | # | # | 1.38 | # | # | # |
| d-fructose 6-phosphate | F6P2− | F6P | 11 | 5.89 | −0.559d | 1.1 | # | 1.74e | −9.72d | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| d-fructose 1,6-phosphate | F16P4− | F16P | 10 | 6.64 | # | 5.92 | # | 2.7 | # | 2.12 | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Fumarate | FUM2− | FUM | 2 | 4.09 | −1.56 | 2.86 | 1.08 | # | # | # | # | # | # | # | # | # | # | # | # | 0.6 | −6.44 | # | # |
| d-glucose 6-phosphate | G6P2− | G6P | 11 | 5.89e | −0.559d | # | # | 1.74b | −9.72d | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| d-glyceraldehyde 3-phosphate | GAP2− | GAP | 5 | 5.27c | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Guanosine diphosphate | GDP3− | GDP | 12 | 6.505 | −2.14 | 2.8 | # | 3.4 | −7.1 | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| d-glucose | GLC0 | GLC | 12 | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Guanosine triphosphate | GTP4− | GTP | 12 | 6.63 | −3 | 2.93 | 7.1 | 4.31 | −17 | 2.31 | # | # | # | # | # | # | # | # | # | 3.7 | # | # | # |
| Water | H2O0 | H2O | 2 | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Isocitrate | ISCIT3− | ISCIT | 5 | 5.765 | # | 4.29 | # | 2.625 | # | 1.43 | # | # | # | # | # | # | # | # | # | 2.54 | # | # | # |
| α-Ketoglutarate | AKG2− | AKG | 4 | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Malate | MAL2− | MAL | 4 | 4.715 | −0.58 | 3.265 | 3.4 | 1.71 | −6.16 | 0.9f | # | # | # | 0.18 | −2.86 | 0.28 | 0.4 | # | # | 2.005 | −1.06 | 1.06 | 8 |
| NADox | NAD−ox | NADox | 26 | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| NADred | NAD2−red | NADred | 27 | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| NADPox | NADP3−ox | NADPox | 25 | 6.255k | # | 3.874k | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| NADPred | NADP4−red | NADPred | 26 | 6.255l | # | 3.874l | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Oxaloacetate | OAA2− | OAA | 2 | 3.9 | 5.24 | 2.26 | 16.62 | 1.02 | # | # | # | # | # | # | # | # | # | # | # | 1.6 | # | # | # |
| Orthophosphate | HPO2−4 | Pi | 1 | 6.78 | 4.6 | 1.945 | −8.7 | 1.823 | −9.518 | 0.669 | # | # | # | 0.5 | # | 0.61 | # | 0.0856 | # | 1.745 | −9.518 | 0.921 | −10.759 |
| 2-Phospho-d-glycerate | PG23− | PG2 | 4 | 7 | # | 3.55 | # | 2.45 | # | # | # | # | # | 1.18 | # | # | # | # | # | # | # | # | # |
| 3-Phospho-d-glycerate | PG33− | PG3 | 4 | 6.89c | # | 3.64g | # | 2.21h | # | # | # | # | # | 0.87 h | # | # | # | # | # | # | # | # | # |
| Phosphoenolpyruvate | PEP3− | PEP | 2 | 6.245 | # | 3.45 | # | 2.26 | # | # | # | # | # | 1.08 | # | # | # | # | # | # | # | # | # |
| Pyruvate | PYR− | PYR | 3 | 2.26 | 12.8 | # | # | 1.1 | # | # | # | # | # | # | # | # | # | # | # | 0.8 | # | # | # |
| Succinate | SUC2− | SUC | 4 | 5.275 | 0.41 | 4.02 | 3 | 1.355 | # | 0.62 | # | # | # | 0.43 | −2.76 | 0.4212 | −2.759 | # | # | 1.405 | −8.939 | 0.65 | −8 |
| Succinyl-CoA | SUCCoA− | SUCCoA | 4 | 3.99c | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Erythrose 4-phosphate | E4P2− | E4P | 9 | 6.255i | −9.75i | 2i | # | 1.58i | −9.71i | # | # | # | # | # | # | # | # | # | # | 1.48i | # | # | # |
| 6-Phosphoglucono-δ-lactone | PGLT2− | PGLT | 11 | 5.99c | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| 6-Phosphogluconate | PGN3− | PGN | 13 | 4.995j | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Ribose 5-phosphate | R5P2− | R5P | 11 | 6.255 | −9.75 | 2 | # | 1.58 | −9.71d | # | # | # | # | # | # | # | # | # | # | 1.48 | # | # | # |
| Ribulose 5-phosphate | RU5P2− | RU5P | 11 | 6.255i | −9.75i | 2i | # | 1.58i | −9.71i | # | # | # | # | # | # | # | # | # | # | 1.48i | # | # | # |
| Sedoheptulose 7-phosphate | S7P2− | S7P | 15 | 6.255i | −9.75i | 2i | # | 1.58i | −9.71i | # | # | # | # | # | # | # | # | # | # | 1.48i | # | # | # |
| Xylulose 5-phosphate | X5P2− | X5P | 11 | 6.255i | −9.75i | 2i | # | 1.58i | −9.71i | # | # | # | # | # | # | # | # | # | # | 1.48i | # | # | # |
| Reactant . | Reference species abbreviationb . | Reactant abbreviation . | NHb . | pKH1 . | pKH2 . | pKMg1 . | pKHMg . | pKMg2 . | pKK1 . | pKNa1 . | pKHNa . | pKCa1 . | pKHCa . | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Acetyl-coenzyme A | ACoA0 | ACoA | 3 | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Adenosine diphosphate | ADP3− | ADP | 12 | 6.496 | −2 | 3.87 | 16 | 3.3 | −15 | 1.59 | −7.5 | 1.27 | −11.76 | 1 | # | 1.12 | # | # | # | 2.86 | −9.6 | 1.48 | −6.2 |
| Adenosine triphosphate | ATP4− | ATP | 12 | 6.71 | −2 | 3.99 | 15 | 4.28 | −18 | 2.32 | −9.6 | 1.7 | −17.52 | 1.17 | −1 | 1.31 | 0.8 | # | # | 3.95 | −13 | 2.16 | −7.9 |
| 1,3-Bisphosphoglycerate | BPG4− | BPG | 4 | 7.1c | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Citrate | CIT3− | CIT | 5 | 5.67 | −1.9 | 4.35 | 3.1 | 3.517 | −8 | 1.8 | # | # | # | 0.6 | −3.54 | 0.75 | −1 | # | # | 3.54 | −1.2 | 2.07 | # |
| Coenzyme A-SH | COAS− | COAS | 0 | 8.17c | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Carbon dioxide (total) | CO2−3 | CO2_tot | 0 | 9.9c | 16.1c | 6.15c | 8.27c | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Dihydroxyacetone phosphate | DHAP2− | DHAP | 5 | 5.9 | # | # | # | 1.57 | # | # | # | # | # | # | # | # | # | # | # | 1.38 | # | # | # |
| d-fructose 6-phosphate | F6P2− | F6P | 11 | 5.89 | −0.559d | 1.1 | # | 1.74e | −9.72d | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| d-fructose 1,6-phosphate | F16P4− | F16P | 10 | 6.64 | # | 5.92 | # | 2.7 | # | 2.12 | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Fumarate | FUM2− | FUM | 2 | 4.09 | −1.56 | 2.86 | 1.08 | # | # | # | # | # | # | # | # | # | # | # | # | 0.6 | −6.44 | # | # |
| d-glucose 6-phosphate | G6P2− | G6P | 11 | 5.89e | −0.559d | # | # | 1.74b | −9.72d | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| d-glyceraldehyde 3-phosphate | GAP2− | GAP | 5 | 5.27c | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Guanosine diphosphate | GDP3− | GDP | 12 | 6.505 | −2.14 | 2.8 | # | 3.4 | −7.1 | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| d-glucose | GLC0 | GLC | 12 | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Guanosine triphosphate | GTP4− | GTP | 12 | 6.63 | −3 | 2.93 | 7.1 | 4.31 | −17 | 2.31 | # | # | # | # | # | # | # | # | # | 3.7 | # | # | # |
| Water | H2O0 | H2O | 2 | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Isocitrate | ISCIT3− | ISCIT | 5 | 5.765 | # | 4.29 | # | 2.625 | # | 1.43 | # | # | # | # | # | # | # | # | # | 2.54 | # | # | # |
| α-Ketoglutarate | AKG2− | AKG | 4 | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Malate | MAL2− | MAL | 4 | 4.715 | −0.58 | 3.265 | 3.4 | 1.71 | −6.16 | 0.9f | # | # | # | 0.18 | −2.86 | 0.28 | 0.4 | # | # | 2.005 | −1.06 | 1.06 | 8 |
| NADox | NAD−ox | NADox | 26 | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| NADred | NAD2−red | NADred | 27 | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| NADPox | NADP3−ox | NADPox | 25 | 6.255k | # | 3.874k | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| NADPred | NADP4−red | NADPred | 26 | 6.255l | # | 3.874l | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Oxaloacetate | OAA2− | OAA | 2 | 3.9 | 5.24 | 2.26 | 16.62 | 1.02 | # | # | # | # | # | # | # | # | # | # | # | 1.6 | # | # | # |
| Orthophosphate | HPO2−4 | Pi | 1 | 6.78 | 4.6 | 1.945 | −8.7 | 1.823 | −9.518 | 0.669 | # | # | # | 0.5 | # | 0.61 | # | 0.0856 | # | 1.745 | −9.518 | 0.921 | −10.759 |
| 2-Phospho-d-glycerate | PG23− | PG2 | 4 | 7 | # | 3.55 | # | 2.45 | # | # | # | # | # | 1.18 | # | # | # | # | # | # | # | # | # |
| 3-Phospho-d-glycerate | PG33− | PG3 | 4 | 6.89c | # | 3.64g | # | 2.21h | # | # | # | # | # | 0.87 h | # | # | # | # | # | # | # | # | # |
| Phosphoenolpyruvate | PEP3− | PEP | 2 | 6.245 | # | 3.45 | # | 2.26 | # | # | # | # | # | 1.08 | # | # | # | # | # | # | # | # | # |
| Pyruvate | PYR− | PYR | 3 | 2.26 | 12.8 | # | # | 1.1 | # | # | # | # | # | # | # | # | # | # | # | 0.8 | # | # | # |
| Succinate | SUC2− | SUC | 4 | 5.275 | 0.41 | 4.02 | 3 | 1.355 | # | 0.62 | # | # | # | 0.43 | −2.76 | 0.4212 | −2.759 | # | # | 1.405 | −8.939 | 0.65 | −8 |
| Succinyl-CoA | SUCCoA− | SUCCoA | 4 | 3.99c | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Erythrose 4-phosphate | E4P2− | E4P | 9 | 6.255i | −9.75i | 2i | # | 1.58i | −9.71i | # | # | # | # | # | # | # | # | # | # | 1.48i | # | # | # |
| 6-Phosphoglucono-δ-lactone | PGLT2− | PGLT | 11 | 5.99c | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| 6-Phosphogluconate | PGN3− | PGN | 13 | 4.995j | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # | # |
| Ribose 5-phosphate | R5P2− | R5P | 11 | 6.255 | −9.75 | 2 | # | 1.58 | −9.71d | # | # | # | # | # | # | # | # | # | # | 1.48 | # | # | # |
| Ribulose 5-phosphate | RU5P2− | RU5P | 11 | 6.255i | −9.75i | 2i | # | 1.58i | −9.71i | # | # | # | # | # | # | # | # | # | # | 1.48i | # | # | # |
| Sedoheptulose 7-phosphate | S7P2− | S7P | 15 | 6.255i | −9.75i | 2i | # | 1.58i | −9.71i | # | # | # | # | # | # | # | # | # | # | 1.48i | # | # | # |
| Xylulose 5-phosphate | X5P2− | X5P | 11 | 6.255i | −9.75i | 2i | # | 1.58i | −9.71i | # | # | # | # | # | # | # | # | # | # | 1.48i | # | # | # |
aDissociation pK and are reported for T = 298.15 K and I = 0.1 M. Unless indicated, values are the average number obtained from NIST database (27). Dissociation enthalpies are reported in units of kJ/mol. Subscripts on ‘pK’ and ‘
’ entries are defined as follows: ‘H’: hydrogen, ‘Mg’: magnesium, ‘K’: potassium, ‘Na’: sodium, ‘Ca’: calcium, ‘1’: first ion dissociation, ‘2’: second ion dissociation, ‘HMg’: hydrogen ion binds to the ligand before magnesium ion binds to the ligand. ‘#’ denotes value is not available.
bAlberty (8).
dTewari et al. (35).
eG6P and F6P are assumed to have equivalent H+ and Mg2+-dissociation properties.
fFrom NIST database (36) at T = 293.15 K.
gLarsson-Raźnikiewicz (37).
hMerrill et al. (38).
iE4P, RU5P, S7P and X5P are assumed to have equivalent dissociation properties as R5P (24).
jCasazza et al. (15).
kBriggs et al. (39).
lNADPred is assumed to have equivalent dissociation properties as NADPox.
Estimation of standard-state thermodynamic quantities
Given the compiled raw experimental data on the reactions and reactants, the thermodynamic model is used to estimate reference and
values for the reference reactions and species. Note that in our thermodynamic model the
values are adjustable parameters estimated to obtain the best fit to the biochemical equilibrium data. As in previous studies (8), values of
for oxidized species of certain redox pairs are arbitrarily set to zero. Thus, these values are not true free energies of the reactions of formation for these chemical species; instead, they are parameters for which the thermodynamic model makes optimal predictions for these interdependent biochemical reactions.
Because the calculated are interrelated [e.g. in the reductive pentose phosphate pathway, five carbon sugars (X5P and R5P) are converted into three carbon (GAP) and six carbon (F6P) sugars which can then be utilized by the pathway of glycolysis], the database of
may be rigorously extended only by recalculating the entire database using all of the raw data. Therefore, model fitting is based on total 686 data entries for the network of all 33 reactions (the first 33 reactions listed in Table 1). Standard free energies of formation for all the reference species are unable to be estimated independently because there are 29 stoichiometrically independent reactions and in total 40 reactants in our system. There are four reactions PDH, IDH2, AKGDH and SDH (last four reactions in Tables 1 and 4) in the TCA cycle for which direct measurements are not available in the literature. For these reactions,
values are calculated using Alberty's database (8) and set as constraints to perform the optimization of the thermodynamic model. IDH2 is not an independent reaction in the overall network of 33 reactions. Therefore, values of
for 32 references species may be estimated from data on the 29 reactions with the three constraints. The values of
for eight species are set to fixed values which are obtained from Alberty (8), as shown in Table 3 (values of
for CoQ0 and CoQH02 do not come into these calculations). A constrained nonlinear optimization procedure with the fmincon solver (Mathworks, Inc.) is used to analyze the whole data set. By weighting in inverse proportion to the number of data points available for a given reaction and minimizing the difference between model predictions and experimental data, a simultaneous solution of standard reaction Gibbs energies is obtained for the entire data set.
Values of (T = 298.15 K, I = 0) used in this study and that were taken from Alberty (8) (Table 3.2)
| Species . | |
|---|---|
| ACoA0 | −188.52 |
| ADP3− | −1906.13 |
| CO2−3 | −527.81 |
| GTP4− | −2768.1 |
| H2O | −237.19 |
| NAD−ox | 0a |
| HPO2−4 | −1096.1 |
| H+ | 0 |
| CoQ0 | 0a |
| CoQH02 | −89.92 |
| Species . | |
|---|---|
| ACoA0 | −188.52 |
| ADP3− | −1906.13 |
| CO2−3 | −527.81 |
| GTP4− | −2768.1 |
| H2O | −237.19 |
| NAD−ox | 0a |
| HPO2−4 | −1096.1 |
| H+ | 0 |
| CoQ0 | 0a |
| CoQH02 | −89.92 |
aProperty value is based on the arbitrary assignment of zero.
Values of (T = 298.15 K, I = 0) used in this study and that were taken from Alberty (8) (Table 3.2)
| Species . | |
|---|---|
| ACoA0 | −188.52 |
| ADP3− | −1906.13 |
| CO2−3 | −527.81 |
| GTP4− | −2768.1 |
| H2O | −237.19 |
| NAD−ox | 0a |
| HPO2−4 | −1096.1 |
| H+ | 0 |
| CoQ0 | 0a |
| CoQH02 | −89.92 |
| Species . | |
|---|---|
| ACoA0 | −188.52 |
| ADP3− | −1906.13 |
| CO2−3 | −527.81 |
| GTP4− | −2768.1 |
| H2O | −237.19 |
| NAD−ox | 0a |
| HPO2−4 | −1096.1 |
| H+ | 0 |
| CoQ0 | 0a |
| CoQH02 | −89.92 |
aProperty value is based on the arbitrary assignment of zero.
Optimal reaction free energies for reference chemical reactions () and for biochemical reactions (
) under physiological conditionsa
| EC No. . | Reaction . | Non-standard element contributionsc . | |||||||
|---|---|---|---|---|---|---|---|---|---|
| T . | I . | pH . | P . | ||||||
| EC 2.7.1.1 | GLK | 16.19 | 16.03 | −19.22 | −35.41 | 1.61 | 1.57 | −41.56 | 2.97 |
| EC 5.3.1.9 | PGI | 3.12 | 3.13 | 2.78 | −0.34 | −0.34 | 0 | 0 | 0 |
| EC 2.7.1.11 | PFK | 26.79 | 26.79 | −15.62 | −42.41 | 1.46 | −4.70 | −41.56 | 2.40 |
| EC 4.1.2.13 | FBA | 18.79 | 18.80 | 24.64 | 5.85 | −1.21 | 6.26 | 0 | 0.81 |
| EC 5.3.1.1 | TPI | −7.01 | −7.01 | −7.57 | −0.56 | −0.39 | 0 | 0 | −0.17 |
| EC 4.1.2.13 | FBA2 | 11.79 | 11.79 | 17.07 | 5.28 | −1.61 | 6.26 | 0 | 0.64 |
| EC 1.2.1.12 | GAP | 51.37 | 51.37 | 2.60 | −48.77 | 2.07 | −9.39 | −41.56 | 0.12 |
| EC 2.7.2.3 | PGK | 34.37 | 34.37 | −19.00 | −53.37 | 1.38 | −9.39 | −41.56 | −3.79 |
| EC 5.4.2.1 | PGYM | −5.89 | −5.90 | −6.35 | −0.46 | −1.37 | 0 | 0 | 0.91 |
| EC 4.2.1.11 | ENO | −4.54 | −4.53 | −4.47 | 0.07 | −0.79 | 0 | 0 | 0.86 |
| EC 2.7.1.40 | PYK | 66.91 | 66.90 | 27.18 | −39.73 | 2.48 | −1.57 | −41.56 | 0.92 |
| EC 4.1.3.7 | CITS | 60.16 | 60.32 | −36.60 | −96.76 | 2.42 | −6.26 | −83.13 | −9.80 |
| EC 4.2.1.3 | ACON | −5.75 | −5.76 | −7.58 | −1.83 | 0.57 | 0 | 0 | −2.41 |
| EC 1.1.1.42 | IDH | 97.05 | 97.06 | −3.29 | −100.34 | 4.80 | −6.26 | −83.13 | −15.76 |
| EC 6.2.1.4 | SCS | −56.55 | −56.56 | 0.07 | 56.62 | −1.03 | 6.26 | 41.56 | 9.82 |
| EC 4.2.1.2 | FUM | −3.38 | −3.38 | −3.52 | −0.14 | 0.39 | 0 | 0 | −0.53 |
| EC 1.1.1.37 | MDH | 71.41 | 71.09 | 28.04 | −43.37 | 0.81 | −3.13 | −41.56 | 0.52 |
| EC 2.7.4.6 | NDK | 0.02 | 0.01 | −0.56 | −0.58 | 0 | 0 | 0 | −0.58 |
| EC 1.6.1.1 | NPTH | −3.53 | −3.58 | −0.41 | 3.12 | 0.02 | 3.13 | 0 | −0.03 |
| EC 1.1.1.40 | MLE | 104.53 | 103.45 | 2.00 | −102.53 | 4.21 | −7.83 | −83.13 | −15.78 |
| EC 1.1.1.37 | MDH2 | 131.57 | 131.41 | −6.50 | −138.07 | 5.30 | −9.39 | −124.69 | −9.28 |
| EC 2.7.1.23 | NADK | 29.11 | 26.90 | −9.95 | −39.06 | 1.17 | −1.57 | −41.56 | 2.89 |
| EC 3.6.1.32 | ATPS | 4.99 | 4.67 | −32.42 | −37.41 | 1.03 | 1.57 | −41.56 | 1.56 |
| EC 3.1.3.1 | G6PH | −11.20 | −11.36 | −13.10 | -1.90 | −0.49 | 0 | 0 | −1.41 |
| EC 6.4.1.1 | PCL | −24.60 | −24.12 | −4.57 | 20.03 | −0.99 | 3.13 | 0 | 17.89 |
| EC 1.1.1.49 | G6PD | 38.69 | #d | −7.51 | −46.20 | 1.56 | −6.26 | −41.56 | 0.07 |
| EC 3.1.1.31 | PGL | 69.16 | #d | −21.89 | −91.05 | 2.78 | −10.96 | −83.13 | 0.25 |
| EC 1.1.1.44 | PGD | 104.64 | #d | 1.23 | −103.41 | 2.70 | −6.26 | −83.13 | −16.73 |
| EC 5.3.1.6 | R5PI | 0.99 | 1.2e | 0.52 | −0.47 | −0.47 | 0 | 0 | 0 |
| EC 5.1.3.1 | RUPE | −1.28 | −1.21e | −1.33 | −0.05 | −0.05 | 0 | 0 | 0 |
| EC 2.2.1.1 | TKL | 1.58 | #d | 1.23 | −0.35 | 0.06 | 0 | 0 | −0.41 |
| EC 2.2.1.2 | TAL | 2.72 | #d | 2.63 | −0.09 | 0.11 | 0 | 0 | −0.20 |
| EC 2.2.1.1 | TKL2 | 8.98 | #d | 8.71 | −0.27 | 0.36 | 0 | 0 | −0.63 |
| EC 1.2.4.1+EC 2.3.1.12+EC 1.8.1.4 | PDH | 15.78f | 17.50 | −39.26 | −55.04 | 0.64 | −4.70 | −41.56 | −9.43 |
| EC 1.1.1.41 | IDH2 | 93.52 | 93.48 | −3.70 | −97.22 | 4.82 | −3.13 | −83.13 | −15.79 |
| EC 1.2.1.52 | AKGDH | 15.85f | 15.28 | −37.66 | −53.51 | 0.64 | −3.13 | −41.56 | −9.45 |
| EC 1.3.5.1 | SDH | −1.35f | −3.10 | −0.59 | 0.76 | −0.05 | 0 | 0 | 0.81 |
| EC No. . | Reaction . | Non-standard element contributionsc . | |||||||
|---|---|---|---|---|---|---|---|---|---|
| T . | I . | pH . | P . | ||||||
| EC 2.7.1.1 | GLK | 16.19 | 16.03 | −19.22 | −35.41 | 1.61 | 1.57 | −41.56 | 2.97 |
| EC 5.3.1.9 | PGI | 3.12 | 3.13 | 2.78 | −0.34 | −0.34 | 0 | 0 | 0 |
| EC 2.7.1.11 | PFK | 26.79 | 26.79 | −15.62 | −42.41 | 1.46 | −4.70 | −41.56 | 2.40 |
| EC 4.1.2.13 | FBA | 18.79 | 18.80 | 24.64 | 5.85 | −1.21 | 6.26 | 0 | 0.81 |
| EC 5.3.1.1 | TPI | −7.01 | −7.01 | −7.57 | −0.56 | −0.39 | 0 | 0 | −0.17 |
| EC 4.1.2.13 | FBA2 | 11.79 | 11.79 | 17.07 | 5.28 | −1.61 | 6.26 | 0 | 0.64 |
| EC 1.2.1.12 | GAP | 51.37 | 51.37 | 2.60 | −48.77 | 2.07 | −9.39 | −41.56 | 0.12 |
| EC 2.7.2.3 | PGK | 34.37 | 34.37 | −19.00 | −53.37 | 1.38 | −9.39 | −41.56 | −3.79 |
| EC 5.4.2.1 | PGYM | −5.89 | −5.90 | −6.35 | −0.46 | −1.37 | 0 | 0 | 0.91 |
| EC 4.2.1.11 | ENO | −4.54 | −4.53 | −4.47 | 0.07 | −0.79 | 0 | 0 | 0.86 |
| EC 2.7.1.40 | PYK | 66.91 | 66.90 | 27.18 | −39.73 | 2.48 | −1.57 | −41.56 | 0.92 |
| EC 4.1.3.7 | CITS | 60.16 | 60.32 | −36.60 | −96.76 | 2.42 | −6.26 | −83.13 | −9.80 |
| EC 4.2.1.3 | ACON | −5.75 | −5.76 | −7.58 | −1.83 | 0.57 | 0 | 0 | −2.41 |
| EC 1.1.1.42 | IDH | 97.05 | 97.06 | −3.29 | −100.34 | 4.80 | −6.26 | −83.13 | −15.76 |
| EC 6.2.1.4 | SCS | −56.55 | −56.56 | 0.07 | 56.62 | −1.03 | 6.26 | 41.56 | 9.82 |
| EC 4.2.1.2 | FUM | −3.38 | −3.38 | −3.52 | −0.14 | 0.39 | 0 | 0 | −0.53 |
| EC 1.1.1.37 | MDH | 71.41 | 71.09 | 28.04 | −43.37 | 0.81 | −3.13 | −41.56 | 0.52 |
| EC 2.7.4.6 | NDK | 0.02 | 0.01 | −0.56 | −0.58 | 0 | 0 | 0 | −0.58 |
| EC 1.6.1.1 | NPTH | −3.53 | −3.58 | −0.41 | 3.12 | 0.02 | 3.13 | 0 | −0.03 |
| EC 1.1.1.40 | MLE | 104.53 | 103.45 | 2.00 | −102.53 | 4.21 | −7.83 | −83.13 | −15.78 |
| EC 1.1.1.37 | MDH2 | 131.57 | 131.41 | −6.50 | −138.07 | 5.30 | −9.39 | −124.69 | −9.28 |
| EC 2.7.1.23 | NADK | 29.11 | 26.90 | −9.95 | −39.06 | 1.17 | −1.57 | −41.56 | 2.89 |
| EC 3.6.1.32 | ATPS | 4.99 | 4.67 | −32.42 | −37.41 | 1.03 | 1.57 | −41.56 | 1.56 |
| EC 3.1.3.1 | G6PH | −11.20 | −11.36 | −13.10 | -1.90 | −0.49 | 0 | 0 | −1.41 |
| EC 6.4.1.1 | PCL | −24.60 | −24.12 | −4.57 | 20.03 | −0.99 | 3.13 | 0 | 17.89 |
| EC 1.1.1.49 | G6PD | 38.69 | #d | −7.51 | −46.20 | 1.56 | −6.26 | −41.56 | 0.07 |
| EC 3.1.1.31 | PGL | 69.16 | #d | −21.89 | −91.05 | 2.78 | −10.96 | −83.13 | 0.25 |
| EC 1.1.1.44 | PGD | 104.64 | #d | 1.23 | −103.41 | 2.70 | −6.26 | −83.13 | −16.73 |
| EC 5.3.1.6 | R5PI | 0.99 | 1.2e | 0.52 | −0.47 | −0.47 | 0 | 0 | 0 |
| EC 5.1.3.1 | RUPE | −1.28 | −1.21e | −1.33 | −0.05 | −0.05 | 0 | 0 | 0 |
| EC 2.2.1.1 | TKL | 1.58 | #d | 1.23 | −0.35 | 0.06 | 0 | 0 | −0.41 |
| EC 2.2.1.2 | TAL | 2.72 | #d | 2.63 | −0.09 | 0.11 | 0 | 0 | −0.20 |
| EC 2.2.1.1 | TKL2 | 8.98 | #d | 8.71 | −0.27 | 0.36 | 0 | 0 | −0.63 |
| EC 1.2.4.1+EC 2.3.1.12+EC 1.8.1.4 | PDH | 15.78f | 17.50 | −39.26 | −55.04 | 0.64 | −4.70 | −41.56 | −9.43 |
| EC 1.1.1.41 | IDH2 | 93.52 | 93.48 | −3.70 | −97.22 | 4.82 | −3.13 | −83.13 | −15.79 |
| EC 1.2.1.52 | AKGDH | 15.85f | 15.28 | −37.66 | −53.51 | 0.64 | −3.13 | −41.56 | −9.45 |
| EC 1.3.5.1 | SDH | −1.35f | −3.10 | −0.59 | 0.76 | −0.05 | 0 | 0 | 0.81 |
aThe physiological conditions (26) are as follows: T = 310.15 K, I = 0.18 M, pH = 7, [Mg2+] = 0.8 mM, [K+] = 140 mM, [Na+] = 10 mM, [Ca2+] = 0.0001 mM. The unit of the free energy is kJ/mol.
b is the optimal reaction free energies for reference chemical reactions in this work,
is the optimal reaction free energies for reference chemical reaction in Li et al. (7).
cThis column lists the actual values of each non-standard physiological condition contribution (in kJ/mol) to the difference between the physiological free energies () and the standard free energies (
). T denotes the temperature contribution, I denotes the ionic strength contribution, pH denotes the pH contribution and P denotes the binding polynomial contribution.
dValue is not available.
eCalculated from Goldberg's database (25): the values for R5P, RU5P and X5P in Goldberg's database are −1582.57, −1581.37 and −1582.58 kJ/mol, respectively.
fValues calculated from Alberty's database (8) are used as model constraints for which there are no equilibrium data in the raw-data database. Since the values for CoQ and CoQH2 are not predicted here, these values are set to 0 and −89.92 kJ/mol, respectively [from Alberty (8)] to computed
for the SDH reaction.
Optimal reaction free energies for reference chemical reactions () and for biochemical reactions (
) under physiological conditionsa
| EC No. . | Reaction . | Non-standard element contributionsc . | |||||||
|---|---|---|---|---|---|---|---|---|---|
| T . | I . | pH . | P . | ||||||
| EC 2.7.1.1 | GLK | 16.19 | 16.03 | −19.22 | −35.41 | 1.61 | 1.57 | −41.56 | 2.97 |
| EC 5.3.1.9 | PGI | 3.12 | 3.13 | 2.78 | −0.34 | −0.34 | 0 | 0 | 0 |
| EC 2.7.1.11 | PFK | 26.79 | 26.79 | −15.62 | −42.41 | 1.46 | −4.70 | −41.56 | 2.40 |
| EC 4.1.2.13 | FBA | 18.79 | 18.80 | 24.64 | 5.85 | −1.21 | 6.26 | 0 | 0.81 |
| EC 5.3.1.1 | TPI | −7.01 | −7.01 | −7.57 | −0.56 | −0.39 | 0 | 0 | −0.17 |
| EC 4.1.2.13 | FBA2 | 11.79 | 11.79 | 17.07 | 5.28 | −1.61 | 6.26 | 0 | 0.64 |
| EC 1.2.1.12 | GAP | 51.37 | 51.37 | 2.60 | −48.77 | 2.07 | −9.39 | −41.56 | 0.12 |
| EC 2.7.2.3 | PGK | 34.37 | 34.37 | −19.00 | −53.37 | 1.38 | −9.39 | −41.56 | −3.79 |
| EC 5.4.2.1 | PGYM | −5.89 | −5.90 | −6.35 | −0.46 | −1.37 | 0 | 0 | 0.91 |
| EC 4.2.1.11 | ENO | −4.54 | −4.53 | −4.47 | 0.07 | −0.79 | 0 | 0 | 0.86 |
| EC 2.7.1.40 | PYK | 66.91 | 66.90 | 27.18 | −39.73 | 2.48 | −1.57 | −41.56 | 0.92 |
| EC 4.1.3.7 | CITS | 60.16 | 60.32 | −36.60 | −96.76 | 2.42 | −6.26 | −83.13 | −9.80 |
| EC 4.2.1.3 | ACON | −5.75 | −5.76 | −7.58 | −1.83 | 0.57 | 0 | 0 | −2.41 |
| EC 1.1.1.42 | IDH | 97.05 | 97.06 | −3.29 | −100.34 | 4.80 | −6.26 | −83.13 | −15.76 |
| EC 6.2.1.4 | SCS | −56.55 | −56.56 | 0.07 | 56.62 | −1.03 | 6.26 | 41.56 | 9.82 |
| EC 4.2.1.2 | FUM | −3.38 | −3.38 | −3.52 | −0.14 | 0.39 | 0 | 0 | −0.53 |
| EC 1.1.1.37 | MDH | 71.41 | 71.09 | 28.04 | −43.37 | 0.81 | −3.13 | −41.56 | 0.52 |
| EC 2.7.4.6 | NDK | 0.02 | 0.01 | −0.56 | −0.58 | 0 | 0 | 0 | −0.58 |
| EC 1.6.1.1 | NPTH | −3.53 | −3.58 | −0.41 | 3.12 | 0.02 | 3.13 | 0 | −0.03 |
| EC 1.1.1.40 | MLE | 104.53 | 103.45 | 2.00 | −102.53 | 4.21 | −7.83 | −83.13 | −15.78 |
| EC 1.1.1.37 | MDH2 | 131.57 | 131.41 | −6.50 | −138.07 | 5.30 | −9.39 | −124.69 | −9.28 |
| EC 2.7.1.23 | NADK | 29.11 | 26.90 | −9.95 | −39.06 | 1.17 | −1.57 | −41.56 | 2.89 |
| EC 3.6.1.32 | ATPS | 4.99 | 4.67 | −32.42 | −37.41 | 1.03 | 1.57 | −41.56 | 1.56 |
| EC 3.1.3.1 | G6PH | −11.20 | −11.36 | −13.10 | -1.90 | −0.49 | 0 | 0 | −1.41 |
| EC 6.4.1.1 | PCL | −24.60 | −24.12 | −4.57 | 20.03 | −0.99 | 3.13 | 0 | 17.89 |
| EC 1.1.1.49 | G6PD | 38.69 | #d | −7.51 | −46.20 | 1.56 | −6.26 | −41.56 | 0.07 |
| EC 3.1.1.31 | PGL | 69.16 | #d | −21.89 | −91.05 | 2.78 | −10.96 | −83.13 | 0.25 |
| EC 1.1.1.44 | PGD | 104.64 | #d | 1.23 | −103.41 | 2.70 | −6.26 | −83.13 | −16.73 |
| EC 5.3.1.6 | R5PI | 0.99 | 1.2e | 0.52 | −0.47 | −0.47 | 0 | 0 | 0 |
| EC 5.1.3.1 | RUPE | −1.28 | −1.21e | −1.33 | −0.05 | −0.05 | 0 | 0 | 0 |
| EC 2.2.1.1 | TKL | 1.58 | #d | 1.23 | −0.35 | 0.06 | 0 | 0 | −0.41 |
| EC 2.2.1.2 | TAL | 2.72 | #d | 2.63 | −0.09 | 0.11 | 0 | 0 | −0.20 |
| EC 2.2.1.1 | TKL2 | 8.98 | #d | 8.71 | −0.27 | 0.36 | 0 | 0 | −0.63 |
| EC 1.2.4.1+EC 2.3.1.12+EC 1.8.1.4 | PDH | 15.78f | 17.50 | −39.26 | −55.04 | 0.64 | −4.70 | −41.56 | −9.43 |
| EC 1.1.1.41 | IDH2 | 93.52 | 93.48 | −3.70 | −97.22 | 4.82 | −3.13 | −83.13 | −15.79 |
| EC 1.2.1.52 | AKGDH | 15.85f | 15.28 | −37.66 | −53.51 | 0.64 | −3.13 | −41.56 | −9.45 |
| EC 1.3.5.1 | SDH | −1.35f | −3.10 | −0.59 | 0.76 | −0.05 | 0 | 0 | 0.81 |
| EC No. . | Reaction . | Non-standard element contributionsc . | |||||||
|---|---|---|---|---|---|---|---|---|---|
| T . | I . | pH . | P . | ||||||
| EC 2.7.1.1 | GLK | 16.19 | 16.03 | −19.22 | −35.41 | 1.61 | 1.57 | −41.56 | 2.97 |
| EC 5.3.1.9 | PGI | 3.12 | 3.13 | 2.78 | −0.34 | −0.34 | 0 | 0 | 0 |
| EC 2.7.1.11 | PFK | 26.79 | 26.79 | −15.62 | −42.41 | 1.46 | −4.70 | −41.56 | 2.40 |
| EC 4.1.2.13 | FBA | 18.79 | 18.80 | 24.64 | 5.85 | −1.21 | 6.26 | 0 | 0.81 |
| EC 5.3.1.1 | TPI | −7.01 | −7.01 | −7.57 | −0.56 | −0.39 | 0 | 0 | −0.17 |
| EC 4.1.2.13 | FBA2 | 11.79 | 11.79 | 17.07 | 5.28 | −1.61 | 6.26 | 0 | 0.64 |
| EC 1.2.1.12 | GAP | 51.37 | 51.37 | 2.60 | −48.77 | 2.07 | −9.39 | −41.56 | 0.12 |
| EC 2.7.2.3 | PGK | 34.37 | 34.37 | −19.00 | −53.37 | 1.38 | −9.39 | −41.56 | −3.79 |
| EC 5.4.2.1 | PGYM | −5.89 | −5.90 | −6.35 | −0.46 | −1.37 | 0 | 0 | 0.91 |
| EC 4.2.1.11 | ENO | −4.54 | −4.53 | −4.47 | 0.07 | −0.79 | 0 | 0 | 0.86 |
| EC 2.7.1.40 | PYK | 66.91 | 66.90 | 27.18 | −39.73 | 2.48 | −1.57 | −41.56 | 0.92 |
| EC 4.1.3.7 | CITS | 60.16 | 60.32 | −36.60 | −96.76 | 2.42 | −6.26 | −83.13 | −9.80 |
| EC 4.2.1.3 | ACON | −5.75 | −5.76 | −7.58 | −1.83 | 0.57 | 0 | 0 | −2.41 |
| EC 1.1.1.42 | IDH | 97.05 | 97.06 | −3.29 | −100.34 | 4.80 | −6.26 | −83.13 | −15.76 |
| EC 6.2.1.4 | SCS | −56.55 | −56.56 | 0.07 | 56.62 | −1.03 | 6.26 | 41.56 | 9.82 |
| EC 4.2.1.2 | FUM | −3.38 | −3.38 | −3.52 | −0.14 | 0.39 | 0 | 0 | −0.53 |
| EC 1.1.1.37 | MDH | 71.41 | 71.09 | 28.04 | −43.37 | 0.81 | −3.13 | −41.56 | 0.52 |
| EC 2.7.4.6 | NDK | 0.02 | 0.01 | −0.56 | −0.58 | 0 | 0 | 0 | −0.58 |
| EC 1.6.1.1 | NPTH | −3.53 | −3.58 | −0.41 | 3.12 | 0.02 | 3.13 | 0 | −0.03 |
| EC 1.1.1.40 | MLE | 104.53 | 103.45 | 2.00 | −102.53 | 4.21 | −7.83 | −83.13 | −15.78 |
| EC 1.1.1.37 | MDH2 | 131.57 | 131.41 | −6.50 | −138.07 | 5.30 | −9.39 | −124.69 | −9.28 |
| EC 2.7.1.23 | NADK | 29.11 | 26.90 | −9.95 | −39.06 | 1.17 | −1.57 | −41.56 | 2.89 |
| EC 3.6.1.32 | ATPS | 4.99 | 4.67 | −32.42 | −37.41 | 1.03 | 1.57 | −41.56 | 1.56 |
| EC 3.1.3.1 | G6PH | −11.20 | −11.36 | −13.10 | -1.90 | −0.49 | 0 | 0 | −1.41 |
| EC 6.4.1.1 | PCL | −24.60 | −24.12 | −4.57 | 20.03 | −0.99 | 3.13 | 0 | 17.89 |
| EC 1.1.1.49 | G6PD | 38.69 | #d | −7.51 | −46.20 | 1.56 | −6.26 | −41.56 | 0.07 |
| EC 3.1.1.31 | PGL | 69.16 | #d | −21.89 | −91.05 | 2.78 | −10.96 | −83.13 | 0.25 |
| EC 1.1.1.44 | PGD | 104.64 | #d | 1.23 | −103.41 | 2.70 | −6.26 | −83.13 | −16.73 |
| EC 5.3.1.6 | R5PI | 0.99 | 1.2e | 0.52 | −0.47 | −0.47 | 0 | 0 | 0 |
| EC 5.1.3.1 | RUPE | −1.28 | −1.21e | −1.33 | −0.05 | −0.05 | 0 | 0 | 0 |
| EC 2.2.1.1 | TKL | 1.58 | #d | 1.23 | −0.35 | 0.06 | 0 | 0 | −0.41 |
| EC 2.2.1.2 | TAL | 2.72 | #d | 2.63 | −0.09 | 0.11 | 0 | 0 | −0.20 |
| EC 2.2.1.1 | TKL2 | 8.98 | #d | 8.71 | −0.27 | 0.36 | 0 | 0 | −0.63 |
| EC 1.2.4.1+EC 2.3.1.12+EC 1.8.1.4 | PDH | 15.78f | 17.50 | −39.26 | −55.04 | 0.64 | −4.70 | −41.56 | −9.43 |
| EC 1.1.1.41 | IDH2 | 93.52 | 93.48 | −3.70 | −97.22 | 4.82 | −3.13 | −83.13 | −15.79 |
| EC 1.2.1.52 | AKGDH | 15.85f | 15.28 | −37.66 | −53.51 | 0.64 | −3.13 | −41.56 | −9.45 |
| EC 1.3.5.1 | SDH | −1.35f | −3.10 | −0.59 | 0.76 | −0.05 | 0 | 0 | 0.81 |
aThe physiological conditions (26) are as follows: T = 310.15 K, I = 0.18 M, pH = 7, [Mg2+] = 0.8 mM, [K+] = 140 mM, [Na+] = 10 mM, [Ca2+] = 0.0001 mM. The unit of the free energy is kJ/mol.
b is the optimal reaction free energies for reference chemical reactions in this work,
is the optimal reaction free energies for reference chemical reaction in Li et al. (7).
cThis column lists the actual values of each non-standard physiological condition contribution (in kJ/mol) to the difference between the physiological free energies () and the standard free energies (
). T denotes the temperature contribution, I denotes the ionic strength contribution, pH denotes the pH contribution and P denotes the binding polynomial contribution.
dValue is not available.
eCalculated from Goldberg's database (25): the values for R5P, RU5P and X5P in Goldberg's database are −1582.57, −1581.37 and −1582.58 kJ/mol, respectively.
fValues calculated from Alberty's database (8) are used as model constraints for which there are no equilibrium data in the raw-data database. Since the values for CoQ and CoQH2 are not predicted here, these values are set to 0 and −89.92 kJ/mol, respectively [from Alberty (8)] to computed
for the SDH reaction.
Results
Estimated Gibbs free energies of reaction and formation
Figure 1 illustrates model predictions versus experimental data for all data used in the analysis. The predicted values are obtained based on accounting for the biochemical state associated with a given experimental measurement in the raw-data database. Data points in the pentose phosphate pathway are shown as filled squares. Other data points are shown as open squares. The data span almost 14 orders of magnitude, and reveal good agreement between model predictions and measured data.
![Model-predicted versus experimental . Model predicted apparent equilibrium constants under defined experimental conditions (T, I, [Mg2+], [Ca2+], [Na+], [K+] and pH) are plotted versus experimental measurements for all data used in the analysis. Data points in the pentose phosphate pathway are shown as filled squares.](https://oupdevcdn.silverchair-staging.com/oup/backfile/Content_public/Journal/database/2011/10.1093/database/bar005/2/m_bar005f1.jpeg?Expires=1772761888&Signature=f3ZKW2L712kIfq~tMdl3VzqKsCo-yUqoaCS41UMyWbpWs0MGVKFIzW~6Om25Z2OBbhptJy2hx4zZO5tcbjiOWiEWRXhJatdFuvKxJQ8yYB1cKQZlcapa9ey2c4yr8o~X0p~EZixyMeddqppoYbrPQvMBzANj5Mln~DOr28b4Wg2kK9dYMRgOIT2-RkLlUqTRYbI1ujbmtYowJlFCMEScDpqEKIHv2lJ9xq1cCUvwDjkbNF2cjEfjfUOTj40J8attSOWHvNbIJ4nvDWFLm6fZssT4n0FY~G04yVautKR6sUjSNs8P-cbwUNo2lYSi0xE~oP29XQDe6H1Qr-L56ZXXRw__&Key-Pair-Id=APKAIYYTVHKX7JZB5EAA)
Model-predicted  versus experimental
versus experimental  . Model predicted apparent equilibrium constants under defined experimental conditions (T, I, [Mg2+], [Ca2+], [Na+], [K+] and pH) are plotted versus experimental measurements for all data used in the analysis. Data points in the pentose phosphate pathway are shown as filled squares.
. Model predicted apparent equilibrium constants under defined experimental conditions (T, I, [Mg2+], [Ca2+], [Na+], [K+] and pH) are plotted versus experimental measurements for all data used in the analysis. Data points in the pentose phosphate pathway are shown as filled squares.
The optimal estimates of listed in Table 4 (
), compared to the values from Li et al. (7) (
).
of first 25 reactions are almost the same as the results obtained previously (7). For the remaining eight reactions of the pentose phosphate pathway, since the
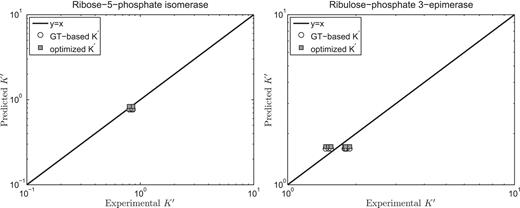
of the reference species for E4P, PGLT, PGN and S7P are not available in the Alberty (8) or Goldberg's database (25), the symbol ‘#’ is used to denote the lack of a value. For reactions R5PI and RUPE, the absolute difference between our current model predictions and the values reported by Goldberg et al. (25) is within a reasonable margin, 0.21 and 0.07 kJ/mol, respectively. Predicted
versus experimental measures are plotted in Figure 2 for these two reactions (R5PI and RUPE). The current database and the Goldberg database yield similar results. Recall that the dissociation properties of R5P, RU5P and X5P are assumed to be the same; the binding polynomials for the reactants on the left- and right-hand sides of these reactions are identical. Thus, the computed apparent equilibrium constants for these reactions do not depend on the experimental ionic composition. The validity of this assumption will be considered in the uncertainty and sensitivity analysis below. In addition, the predicted thermodynamic properties are not affected by the ionic strength for these reactions.
Optimal predicted associated with the
predictions are listed in Table 5, compared to the optimal values of our previous version of the database (7). After the seven reactants of the pentose phosphate pathway and three constraints (
of reaction PDH, AKGDH and SDH) are introduced, most of the estimated values of
are shifted substantially. However, from Table 4 we can see that these shifts do not change the predicted
compared to previous predictions. This is because the shifts in
do not change the optimized results (apparent
or
) of our model. Recall that here the estimated
values represent parameters in a thermodynamic model for this set of interdependent biochemical reactions. Since the number of independent reactions for which data exist (29 reactions) is smaller than the number of
values to represent the system (40 reactants), values for several reference species are set to either existing values or values reported elsewhere (Table 3). As a result, these
values are not physical constants. Rather, they are parameters in a thermodynamic network model that together form a self-consistent picture of the thermodynamics of reactions of the set of reactants studied here.
| No. . | Species . | Sensitivity . | |||
|---|---|---|---|---|---|
| 1 | GLC0 | −719.37 | −916.39 | 197.02 | 0.33 |
| 2 | ATP4− | −2770.03 | −2769.71 | 0.32 | 56099.52 |
| 3 | F6P2− | −1563.96 | −1760.81 | 196.85 | 1.52 |
| 4 | F16P4− | −2401.08 | −2597.60 | 196.52 | 3.55 |
| 5 | DHAP2− | −1194.65 | −1292.91 | 98.26 | 3.51 |
| 6 | GAP2− | −1187.64 | −1285.90 | 98.26 | 3.49 |
| 7 | BPG4− | −2276.28 | −2354.55 | 78.27 | 19.44 |
| 8 | NAD2−red | 43.91 | 23.91 | 20.00 | 0.14 |
| 9 | PG33− | −1429.38 | −1507.96 | 78.58 | 7.83 |
| 10 | PG23− | −1423.49 | −1502.06 | 78.57 | 7.83 |
| 11 | PEP3− | −1190.84 | −1269.40 | 78.56 | 5.54 |
| 12 | PYR− | −393.85 | −472.72 | 78.87 | 0.64 |
| 13 | OAA2− | −714.06 | −792.13 | 78.07 | 2.06 |
| 14 | CIT3− | −1022.44 | −1157.52 | 135.08 | 1.38 |
| 15 | ISCIT3− | −1016.69 | −1151.76 | 135.07 | 1.38 |
| 16 | NADP3−ox | −834.79 | −836.68 | 1.89 | 1837.57 |
| 17 | AKG2− | −676.45 | −791.57 | 115.12 | 0.83 |
| 18 | SUC2− | −589.56 | −685.56 | 96.00 | 0.91 |
| 19 | GDP3− | −1904.22 | −1904.53 | 0.31 | 9560.62 |
| 20 | FUM2− | −500.99 | −598.74 | 97.75 | 0.67 |
| 21 | MAL2− | −741.56 | −839.30 | 97.74 | 1.44 |
| 22 | G6P2− | −1567.08 | −1763.94b | 196.86 | 1.52 |
| 23 | COAS0 | −57.17 | 0b | 57.17 | 0.03 |
| 24 | NADP4−red | −787.35 | −809.19b | 21.84 | 41.94 |
| 25 | SUCCoA− | −471.06 | −509.59b | 38.53 | 3.47 |
| 26 | E4P2− | −1306.62 | # | # | 2.39 |
| 27 | PGLT2− | −1575.83 | # | # | 1.85 |
| 28 | PGN3− | −1782.55 | # | # | 2.34 |
| 29 | R5P2− | −1435.72 | # | # | 1.86 |
| 30 | RU5P2− | −1434.72 | # | # | 1.86 |
| 31 | S7P2− | −1685.66 | # | # | 1.31 |
| 32 | X5P2− | −1436.00 | # | # | 1.85 |
| No. . | Species . | Sensitivity . | |||
|---|---|---|---|---|---|
| 1 | GLC0 | −719.37 | −916.39 | 197.02 | 0.33 |
| 2 | ATP4− | −2770.03 | −2769.71 | 0.32 | 56099.52 |
| 3 | F6P2− | −1563.96 | −1760.81 | 196.85 | 1.52 |
| 4 | F16P4− | −2401.08 | −2597.60 | 196.52 | 3.55 |
| 5 | DHAP2− | −1194.65 | −1292.91 | 98.26 | 3.51 |
| 6 | GAP2− | −1187.64 | −1285.90 | 98.26 | 3.49 |
| 7 | BPG4− | −2276.28 | −2354.55 | 78.27 | 19.44 |
| 8 | NAD2−red | 43.91 | 23.91 | 20.00 | 0.14 |
| 9 | PG33− | −1429.38 | −1507.96 | 78.58 | 7.83 |
| 10 | PG23− | −1423.49 | −1502.06 | 78.57 | 7.83 |
| 11 | PEP3− | −1190.84 | −1269.40 | 78.56 | 5.54 |
| 12 | PYR− | −393.85 | −472.72 | 78.87 | 0.64 |
| 13 | OAA2− | −714.06 | −792.13 | 78.07 | 2.06 |
| 14 | CIT3− | −1022.44 | −1157.52 | 135.08 | 1.38 |
| 15 | ISCIT3− | −1016.69 | −1151.76 | 135.07 | 1.38 |
| 16 | NADP3−ox | −834.79 | −836.68 | 1.89 | 1837.57 |
| 17 | AKG2− | −676.45 | −791.57 | 115.12 | 0.83 |
| 18 | SUC2− | −589.56 | −685.56 | 96.00 | 0.91 |
| 19 | GDP3− | −1904.22 | −1904.53 | 0.31 | 9560.62 |
| 20 | FUM2− | −500.99 | −598.74 | 97.75 | 0.67 |
| 21 | MAL2− | −741.56 | −839.30 | 97.74 | 1.44 |
| 22 | G6P2− | −1567.08 | −1763.94b | 196.86 | 1.52 |
| 23 | COAS0 | −57.17 | 0b | 57.17 | 0.03 |
| 24 | NADP4−red | −787.35 | −809.19b | 21.84 | 41.94 |
| 25 | SUCCoA− | −471.06 | −509.59b | 38.53 | 3.47 |
| 26 | E4P2− | −1306.62 | # | # | 2.39 |
| 27 | PGLT2− | −1575.83 | # | # | 1.85 |
| 28 | PGN3− | −1782.55 | # | # | 2.34 |
| 29 | R5P2− | −1435.72 | # | # | 1.86 |
| 30 | RU5P2− | −1434.72 | # | # | 1.86 |
| 31 | S7P2− | −1685.66 | # | # | 1.31 |
| 32 | X5P2− | −1436.00 | # | # | 1.85 |
| No. . | Species . | Sensitivity . | |||
|---|---|---|---|---|---|
| 1 | GLC0 | −719.37 | −916.39 | 197.02 | 0.33 |
| 2 | ATP4− | −2770.03 | −2769.71 | 0.32 | 56099.52 |
| 3 | F6P2− | −1563.96 | −1760.81 | 196.85 | 1.52 |
| 4 | F16P4− | −2401.08 | −2597.60 | 196.52 | 3.55 |
| 5 | DHAP2− | −1194.65 | −1292.91 | 98.26 | 3.51 |
| 6 | GAP2− | −1187.64 | −1285.90 | 98.26 | 3.49 |
| 7 | BPG4− | −2276.28 | −2354.55 | 78.27 | 19.44 |
| 8 | NAD2−red | 43.91 | 23.91 | 20.00 | 0.14 |
| 9 | PG33− | −1429.38 | −1507.96 | 78.58 | 7.83 |
| 10 | PG23− | −1423.49 | −1502.06 | 78.57 | 7.83 |
| 11 | PEP3− | −1190.84 | −1269.40 | 78.56 | 5.54 |
| 12 | PYR− | −393.85 | −472.72 | 78.87 | 0.64 |
| 13 | OAA2− | −714.06 | −792.13 | 78.07 | 2.06 |
| 14 | CIT3− | −1022.44 | −1157.52 | 135.08 | 1.38 |
| 15 | ISCIT3− | −1016.69 | −1151.76 | 135.07 | 1.38 |
| 16 | NADP3−ox | −834.79 | −836.68 | 1.89 | 1837.57 |
| 17 | AKG2− | −676.45 | −791.57 | 115.12 | 0.83 |
| 18 | SUC2− | −589.56 | −685.56 | 96.00 | 0.91 |
| 19 | GDP3− | −1904.22 | −1904.53 | 0.31 | 9560.62 |
| 20 | FUM2− | −500.99 | −598.74 | 97.75 | 0.67 |
| 21 | MAL2− | −741.56 | −839.30 | 97.74 | 1.44 |
| 22 | G6P2− | −1567.08 | −1763.94b | 196.86 | 1.52 |
| 23 | COAS0 | −57.17 | 0b | 57.17 | 0.03 |
| 24 | NADP4−red | −787.35 | −809.19b | 21.84 | 41.94 |
| 25 | SUCCoA− | −471.06 | −509.59b | 38.53 | 3.47 |
| 26 | E4P2− | −1306.62 | # | # | 2.39 |
| 27 | PGLT2− | −1575.83 | # | # | 1.85 |
| 28 | PGN3− | −1782.55 | # | # | 2.34 |
| 29 | R5P2− | −1435.72 | # | # | 1.86 |
| 30 | RU5P2− | −1434.72 | # | # | 1.86 |
| 31 | S7P2− | −1685.66 | # | # | 1.31 |
| 32 | X5P2− | −1436.00 | # | # | 1.85 |
| No. . | Species . | Sensitivity . | |||
|---|---|---|---|---|---|
| 1 | GLC0 | −719.37 | −916.39 | 197.02 | 0.33 |
| 2 | ATP4− | −2770.03 | −2769.71 | 0.32 | 56099.52 |
| 3 | F6P2− | −1563.96 | −1760.81 | 196.85 | 1.52 |
| 4 | F16P4− | −2401.08 | −2597.60 | 196.52 | 3.55 |
| 5 | DHAP2− | −1194.65 | −1292.91 | 98.26 | 3.51 |
| 6 | GAP2− | −1187.64 | −1285.90 | 98.26 | 3.49 |
| 7 | BPG4− | −2276.28 | −2354.55 | 78.27 | 19.44 |
| 8 | NAD2−red | 43.91 | 23.91 | 20.00 | 0.14 |
| 9 | PG33− | −1429.38 | −1507.96 | 78.58 | 7.83 |
| 10 | PG23− | −1423.49 | −1502.06 | 78.57 | 7.83 |
| 11 | PEP3− | −1190.84 | −1269.40 | 78.56 | 5.54 |
| 12 | PYR− | −393.85 | −472.72 | 78.87 | 0.64 |
| 13 | OAA2− | −714.06 | −792.13 | 78.07 | 2.06 |
| 14 | CIT3− | −1022.44 | −1157.52 | 135.08 | 1.38 |
| 15 | ISCIT3− | −1016.69 | −1151.76 | 135.07 | 1.38 |
| 16 | NADP3−ox | −834.79 | −836.68 | 1.89 | 1837.57 |
| 17 | AKG2− | −676.45 | −791.57 | 115.12 | 0.83 |
| 18 | SUC2− | −589.56 | −685.56 | 96.00 | 0.91 |
| 19 | GDP3− | −1904.22 | −1904.53 | 0.31 | 9560.62 |
| 20 | FUM2− | −500.99 | −598.74 | 97.75 | 0.67 |
| 21 | MAL2− | −741.56 | −839.30 | 97.74 | 1.44 |
| 22 | G6P2− | −1567.08 | −1763.94b | 196.86 | 1.52 |
| 23 | COAS0 | −57.17 | 0b | 57.17 | 0.03 |
| 24 | NADP4−red | −787.35 | −809.19b | 21.84 | 41.94 |
| 25 | SUCCoA− | −471.06 | −509.59b | 38.53 | 3.47 |
| 26 | E4P2− | −1306.62 | # | # | 2.39 |
| 27 | PGLT2− | −1575.83 | # | # | 1.85 |
| 28 | PGN3− | −1782.55 | # | # | 2.34 |
| 29 | R5P2− | −1435.72 | # | # | 1.86 |
| 30 | RU5P2− | −1434.72 | # | # | 1.86 |
| 31 | S7P2− | −1685.66 | # | # | 1.31 |
| 32 | X5P2− | −1436.00 | # | # | 1.85 |
Predicted apparent Gibbs free energies under physiology conditions
The contributions of non-standard elements to the differences between the standard free energy for the reference chemical reaction () and the physiological energy values (
) are listed in the last four columns of Table 4. The results can be divided to three cases: (i) if the stoichiometric coefficient of H+ is non-zero in the reference chemical reaction (vH ≠ 0), the differences are substantial and pH contributes significantly, accounting for at least 73% of the difference, e.g. reactions GLK, PFK and GAP; (ii) if vH = 0 (
) and
(
), the differences tend to be relatively small compared with case (i) and temperature and/or binding polynomials contribute most to the differences, e.g. reactions PGI, TPI and ACON; (iii) if vH = 0 (
) and
ionic strength and/or binding polynomials contribute most to the differences, e.g. reactions FBA, NPTH and PCL.
For the reactions of the pentose phosphate pathway, only the first three reactions G6PD, PGL and PGD show substantial difference between free energy for the reference chemical reaction () and for biochemical reaction (
) under physiological conditions. These three reactions have vH ≠ 0. They are the oxidative portion of the pentose phosphate pathway (15, 23), which produce NADPred and are essentially ‘irreversible’ in vivo (23).
Dissociation constants uncertainty and sensitivity analysis
The pK values listed in Table 2 are taken as the average value when there are several values (≥2) available in NIST database (27). For these pK values, the average value may not represent the best choice to be used in the model, i.e. some value among those available values may be more accurate than others. For some pK values, there exists only one estimate or no direct estimates. In order to predict the impact of uncertainty of these values on the model output, an uncertainty and sensitivity analysis is performed.
Dissociation constants uncertainty analysis for reactants with several pK values available in NIST database (27)
| Reactant abbreviation . | ||||
|---|---|---|---|---|
| ADP | 0.0539 | 0.0545 | 0.01748 | |
| ATP | 0.0849 | 0.1051 | 0.1215 | |
| CIT | 0.0423 | 0.0597 | 0.0480 | |
| GDP | 0.0630 | |||
| GTP | 0.0799 | 0.0835 | ||
| ISCIT | 0.0052 | 0.0571 | ||
| MAL | 0.0148 | 0.0153 | 0.0549 | |
| Pi | 0.0251 | 0.0463 | 0.1975 | 0.1433 |
| PEP | 0.0336 | |||
| SUC | 0.0133 | 0.0149 | 0.1476 | |
| R5P | 0.0016 |
| Reactant abbreviation . | ||||
|---|---|---|---|---|
| ADP | 0.0539 | 0.0545 | 0.01748 | |
| ATP | 0.0849 | 0.1051 | 0.1215 | |
| CIT | 0.0423 | 0.0597 | 0.0480 | |
| GDP | 0.0630 | |||
| GTP | 0.0799 | 0.0835 | ||
| ISCIT | 0.0052 | 0.0571 | ||
| MAL | 0.0148 | 0.0153 | 0.0549 | |
| Pi | 0.0251 | 0.0463 | 0.1975 | 0.1433 |
| PEP | 0.0336 | |||
| SUC | 0.0133 | 0.0149 | 0.1476 | |
| R5P | 0.0016 |
Dissociation constants uncertainty analysis for reactants with several pK values available in NIST database (27)
| Reactant abbreviation . | ||||
|---|---|---|---|---|
| ADP | 0.0539 | 0.0545 | 0.01748 | |
| ATP | 0.0849 | 0.1051 | 0.1215 | |
| CIT | 0.0423 | 0.0597 | 0.0480 | |
| GDP | 0.0630 | |||
| GTP | 0.0799 | 0.0835 | ||
| ISCIT | 0.0052 | 0.0571 | ||
| MAL | 0.0148 | 0.0153 | 0.0549 | |
| Pi | 0.0251 | 0.0463 | 0.1975 | 0.1433 |
| PEP | 0.0336 | |||
| SUC | 0.0133 | 0.0149 | 0.1476 | |
| R5P | 0.0016 |
| Reactant abbreviation . | ||||
|---|---|---|---|---|
| ADP | 0.0539 | 0.0545 | 0.01748 | |
| ATP | 0.0849 | 0.1051 | 0.1215 | |
| CIT | 0.0423 | 0.0597 | 0.0480 | |
| GDP | 0.0630 | |||
| GTP | 0.0799 | 0.0835 | ||
| ISCIT | 0.0052 | 0.0571 | ||
| MAL | 0.0148 | 0.0153 | 0.0549 | |
| Pi | 0.0251 | 0.0463 | 0.1975 | 0.1433 |
| PEP | 0.0336 | |||
| SUC | 0.0133 | 0.0149 | 0.1476 | |
| R5P | 0.0016 |
| Reactant abbreviation . | ||||
|---|---|---|---|---|
| ADP | 0.4936 | 0.3696 | 0.1709 | |
| ATP | 0.2151 | 0.2665 | 0.2210 | |
| CIT | 0.6029 | |||
| COAS | 0.5344 | |||
| DHAP | 0.6591 | 0.3772 | ||
| F16P | 1.1839 | 0.3181 | 1.3545 | |
| G6P | 0.6372 | 0.4524 | ||
| GDP | 0.1873 | |||
| GTP | 0.1310 | |||
| ISCIT | 0.1230 | 0.2245 | ||
| NADPox | 1.7916 | |||
| NADPred | 0.7611 | |||
| Pi | 0.1248 | 0.2015 | ||
| PG2 | 1.2172 | |||
| PG3 | 0.3698 | |||
| PEP | 0.2293 | |||
| R5P | 0.1818 | |||
| RU5P | 0.1007 | |||
| S7P | 0.1433 | |||
| X5P | 0.1597 |
| Reactant abbreviation . | ||||
|---|---|---|---|---|
| ADP | 0.4936 | 0.3696 | 0.1709 | |
| ATP | 0.2151 | 0.2665 | 0.2210 | |
| CIT | 0.6029 | |||
| COAS | 0.5344 | |||
| DHAP | 0.6591 | 0.3772 | ||
| F16P | 1.1839 | 0.3181 | 1.3545 | |
| G6P | 0.6372 | 0.4524 | ||
| GDP | 0.1873 | |||
| GTP | 0.1310 | |||
| ISCIT | 0.1230 | 0.2245 | ||
| NADPox | 1.7916 | |||
| NADPred | 0.7611 | |||
| Pi | 0.1248 | 0.2015 | ||
| PG2 | 1.2172 | |||
| PG3 | 0.3698 | |||
| PEP | 0.2293 | |||
| R5P | 0.1818 | |||
| RU5P | 0.1007 | |||
| S7P | 0.1433 | |||
| X5P | 0.1597 |
| Reactant abbreviation . | ||||
|---|---|---|---|---|
| ADP | 0.4936 | 0.3696 | 0.1709 | |
| ATP | 0.2151 | 0.2665 | 0.2210 | |
| CIT | 0.6029 | |||
| COAS | 0.5344 | |||
| DHAP | 0.6591 | 0.3772 | ||
| F16P | 1.1839 | 0.3181 | 1.3545 | |
| G6P | 0.6372 | 0.4524 | ||
| GDP | 0.1873 | |||
| GTP | 0.1310 | |||
| ISCIT | 0.1230 | 0.2245 | ||
| NADPox | 1.7916 | |||
| NADPred | 0.7611 | |||
| Pi | 0.1248 | 0.2015 | ||
| PG2 | 1.2172 | |||
| PG3 | 0.3698 | |||
| PEP | 0.2293 | |||
| R5P | 0.1818 | |||
| RU5P | 0.1007 | |||
| S7P | 0.1433 | |||
| X5P | 0.1597 |
| Reactant abbreviation . | ||||
|---|---|---|---|---|
| ADP | 0.4936 | 0.3696 | 0.1709 | |
| ATP | 0.2151 | 0.2665 | 0.2210 | |
| CIT | 0.6029 | |||
| COAS | 0.5344 | |||
| DHAP | 0.6591 | 0.3772 | ||
| F16P | 1.1839 | 0.3181 | 1.3545 | |
| G6P | 0.6372 | 0.4524 | ||
| GDP | 0.1873 | |||
| GTP | 0.1310 | |||
| ISCIT | 0.1230 | 0.2245 | ||
| NADPox | 1.7916 | |||
| NADPred | 0.7611 | |||
| Pi | 0.1248 | 0.2015 | ||
| PG2 | 1.2172 | |||
| PG3 | 0.3698 | |||
| PEP | 0.2293 | |||
| R5P | 0.1818 | |||
| RU5P | 0.1007 | |||
| S7P | 0.1433 | |||
| X5P | 0.1597 |
The product (US) combining uncertainty U and sensitivity S can be used to check the overlapping effect of uncertainty and sensitivity. For example, recall that we arbitrarily assign the value of 4.995 to the pKH1 for PGN. Since the value is not available in NIST database, its uncertainty U is set to the average number 0.0609. If we consider the theoretical range of 4–5.99 discussed above, then the calculated uncertainty U is ∼0.4. For this case, because the computed pKH1 sensitivity is 0.0225, the US product is <0.01, which is small enough that the value of pKH1 for PGN has no substantial effect on the model output. Similarly, recall that E4P, RU5P, S7P and X5P are assumed to have dissociation properties equivalent to R5P in our calculations. Although the computed pK sensitivities of E4P, RU5P, S7P and X5P are 3.81E-6, 0.1007, 0.1433 and 0.1597, respectively, all the US products of the pKH1 for these reactants are <0.01. Therefore, the assumption of equivalent dissociation properties for E4P, R5P, RU5P, S7P and X5P does not substantially effect our calculations.
Figure 3A illustrates that US products span eight orders of magnitude. Figure 3B illustrates the detailed distribution of the US products >0.01. All US products are <0.11. There are 23 cases for which US >0.01. These 23 US values belong to 15 reactants and four pKs as listed in Table 8. They are a subset of the pKs with sensitivity >0.1. They demonstrate the most important pKs which can make obvious impact on the model output. The largest four US values are as indicated in Figure 3B.
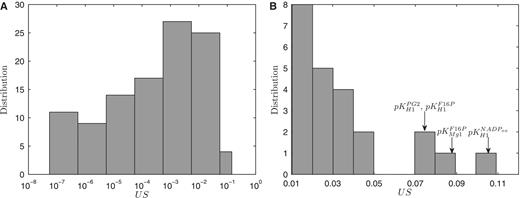
(A) Distribution of the product of uncertainty and sensitivity (US) for all pK values; (B) detailed distribution of the product >0.01.
The product () >0.01 in dissociation constants uncertainty and sensitivity analysis
| Reactant abbreviation . | |
|---|---|
| ADP | |
| ATP | |
| CIT | |
| COAS | |
| DHAP | |
| F16P | |
| G6P | |
| GDP | |
| GTP | |
| ISCIT | |
| Pi | |
| NADPox | |
| NADPred | |
| PG2 | |
| PG3 |
| Reactant abbreviation . | |
|---|---|
| ADP | |
| ATP | |
| CIT | |
| COAS | |
| DHAP | |
| F16P | |
| G6P | |
| GDP | |
| GTP | |
| ISCIT | |
| Pi | |
| NADPox | |
| NADPred | |
| PG2 | |
| PG3 |
The product () >0.01 in dissociation constants uncertainty and sensitivity analysis
| Reactant abbreviation . | |
|---|---|
| ADP | |
| ATP | |
| CIT | |
| COAS | |
| DHAP | |
| F16P | |
| G6P | |
| GDP | |
| GTP | |
| ISCIT | |
| Pi | |
| NADPox | |
| NADPred | |
| PG2 | |
| PG3 |
| Reactant abbreviation . | |
|---|---|
| ADP | |
| ATP | |
| CIT | |
| COAS | |
| DHAP | |
| F16P | |
| G6P | |
| GDP | |
| GTP | |
| ISCIT | |
| Pi | |
| NADPox | |
| NADPred | |
| PG2 | |
| PG3 |
Database dissemination
ThermoML is an extensible markup language (XML)-based approach, which is an IUPAC standard for storage and exchange of thermodynamic property data (29–32). Our optimized results are stored in the standard ThermoML format with two small extensions to the current ThermoML schema (32): (i) adding ‘pseudo-Gibbs free energy of formation, kJ/mol’ in the list of ePropName in BioProperties of PureOrMixtureData; and (ii) adding ‘biochemical network calculation’ in ePredictionType of Prediction. We use the term ‘pseudo-Gibbs free energy of formation’ because in our thermodynamic model the estimated values represent adjustable parameters for the given set of interdependent biochemical reactions. In our ThermoML data files, the abbreviation name of reactant is also added in sCommonName in Compound. In the ThermoML reaction database, if the value of
is not available, it is specified in sPredictionMethodDescription, and both nPropValue and nPropDigits are set to 0 in PropertyValue of NumValues. The ThermoML schema and our ThermoML data files are provided in Supplementary Data.
Discussion
We have updated our biochemical thermodynamic database by adding the reactions of the pentose phosphate pathway. To build the new database, each original publication has been studied on a case-by-case basis, case-specific assumptions and approximations determined and documented, and case-specific calculations performed and documented. Raw data and documented estimations of solution properties are made electronically available so that the updated database remains transparent and extensible.
The developed database is optimally self-consistent and consistent with the data available for reactions considered and the constraints. Theoretical predictions of apparent equilibrium constants optimally match experimental data on equilibrium constants. These apparent equilibrium constants are predicted based on the estimated species-level Gibbs free energies of formation and accounting for the effects of temperature, ionic interactions and hydrogen and metal cation binding. The new database provides thermodynamic and network-based estimates of thermodynamic properties for six reactions of the pentose phosphate pathway for which estimates are not available in the pre-existing literature.
These calculations demonstrate how network thermodynamic calculations are effectively extended. Adding raw experimental data on reactions and reactants of the pentose phosphate pathway into corresponding raw-data database, reaction database and reactant database, respectively, a previous thermodynamic network model was extended to include these elements.
Although the new optimal estimates of for reactants of glycolysis and tricarboxylic acid cycle are equal to previous estimates (7), most of the optimal predicted
values which are associated with the
predictions are shifted compared to the previous version. This result demonstrates that reliable and self-consistent extensions require the recalculation of entire set of species-level parameters. Furthermore, sensitivity analysis reveals that some formation energies can vary substantially without changing the optimized objective value significantly. While this set of optimal values represents a self-consistent set, combining these estimated formation energies with independently estimated parameters from other studies would require re-optimizing a combined database.
The uncertainty and sensitivity analysis of dissociation constants reveals 23 pKs most important to the model output. Additional experimental measurements of these parameter values are desirable.
Supplementary Data
Supplementary data are available at Database Online.
Acknowledgements
The authors are grateful to Robert Goldberg for advice and critical comments.
Funding
National Institutes of Health Heart Lung and Blood Institute (grant number HL072011). Funding for open access charge: National Institutes of Health Heart Lung and Blood Institute.
Conflict of interest. None declared.
References
Appendix A
Calculating the physiological free energy ![formula]()
Example
Nomenclature
B: an empirical constant taken to be 1.6 M−1/2
E: the minimum squared difference between model simulations and experimental data
: standard Gibbs free energy of reaction
: standard Gibbs free energy of formation of species i
: apparent Gibbs free energy of reaction
: enthalpy of proton/metal cation dissociation
: standard enthalpy of reaction
I: ionic strength
K: chemical (reference reaction) equilibrium constant
: apparent equilibrium constant
Kdi: the dissociation constant of cation ion d
M: the number of reactions
N: the number of pKs which have several values available in NIST database
Nj: the number of experimental data in each reaction
Pj: binding polynomial associated with reactant j
pK: negative logarithm of the dissociation constant
R: gas constant, 8.3145 J K−1 mol−1
S: sensitivity
T: temperature
U: uncertainty
vi: stoichiometric coefficient for species i in a given reaction
zi: valence of species i
: the ionic strength contribution
: the pH contribution
: the binding polynomial contribution
: the temperature contribution