-
PDF
- Split View
-
Views
-
Cite
Cite
Dina Sokol, Firat Atagun, TRedD—A database for tandem repeats over the edit distance, Database, Volume 2010, 2010, baq003, https://doi.org/10.1093/database/baq003
Close - Share Icon Share
Abstract
A ‘tandem repeat’ in DNA is a sequence of two or more contiguous, approximate copies of a pattern of nucleotides. Tandem repeats are common in the genomes of both eukaryotic and prokaryotic organisms. They are significant markers for human identity testing, disease diagnosis, sequence homology and population studies. In this article, we describe a new database, TRedD, which contains the tandem repeats found in the human genome. The database is publicly available online, and the software for locating the repeats is also freely available. The definition of tandem repeats used by TRedD is a new and innovative definition based upon the concept of ‘evolutive tandem repeats’. In addition, we have developed a tool, called TandemGraph, to graphically depict the repeats occurring in a sequence. This tool can be coupled with any repeat finding software, and it should greatly facilitate analysis of results.
Database URL:http://tandem.sci.brooklyn.cuny.edu/
Introduction
A ‘tandem repeat’ in DNA is a sequence of two or more contiguous, approximate copies of a pattern of nucleotides. Tandem repeats are common in the genomes of both eukaryotic and prokaryotic organisms. They are significant markers for human identity testing, disease diagnosis, sequence homology and population studies.
DNA consisting of tandem repeats is also called ‘satellite DNA’. Satellite DNA is usually classified among ‘satellites’ (spanning megabases of DNA), ‘minisatellites’ (repeat units in the range 10–60 bp, spanning 1–20 kb) and microsatellites (repeat units in the range 1–6 bp, spanning <150 bases). The minisatellites are also called ‘Variable Number Tandem Repeats’ or VNTRs and the microsatellites are often referred to as ‘Short Tandem Repeats’ or STRs.
Tandem repeats are responsible for over 30 inherited diseases in humans. Expansions of simple DNA repeats have been linked to hereditary disorders in humans, including fragile X syndrome, myotonic dystrophy, Huntington's disease, various spinocerebellar ataxias, Friedreich's ataxia and others (1). These diseases are sometimes called the ‘repeat expansion diseases’ since they are caused by long and highly polymorphic tandem repeats (2, 3).
The repeats in the human genome are the genetic markers used in DNA forensics (4). Since the number of adjacent repeated units varies from individual to individual, the copy number of a tandem repeat can be used to identify an individual, and relations such as parent or grandparent. Tandem repeats are also used in population studies (5), conservation biology (6) and in conjunction with multiple sequence alignments (7, 8).
Tandem repeats are found in both coding and non-coding regions of DNA. Expansions of repeats found in the protein-coding portions of genes can affect the function of the gene by causing synthesis of malfunctioning proteins. Repeats in non-coding regions have been shown to affect biological processes by affecting gene expression, transcription and translation.
Due to the sequencing of the human genome by the Human Genome Project (9, 10), it is now possible to analyze the sequence of the human genome and create a listing of all tandem repeats in the genome. Some existing software tools for finding tandem repeats in a sequence include: TRF (Tandem Repeats Finder) (11), mreps (12), ATRHunter (13), STRING (14) and TandemSWAN (15). There are several online databases for tandem repeats, most notably TRDB (16) and STRBase (for Short Tandem Repeats) (17). TRbase (18) is a database that relates tandem repeats to disease genes for the human genome.
One of the difficulties involved in locating tandem repeats is in accurately defining a tandem repeat. Exact repeats, i.e. repeats that do not allow any errors, are clearly defined. Once we introduce errors, such as insertions and deletions of single or multiple bases, we have to define what constitutes a tandem repeat. Each of the tools for locating tandem repeats relies on certain assumptions and definitions. Thus, the output of the different tools differs, each offering insights into the presence of repeated sequences.
Sokol et al. (19) have presented a precise definition of a tandem repeat over the edit distance, where the edit distance allows insertions, deletions and mismatches, each at a cost of 1. An efficient, deterministic algorithm that locates all tandem repeats within a sequence, over the edit distance, was presented. Furthermore, Sokol's research team at Brooklyn College have recently developed TRed—software for locating tandem repeats over the edit distance within a DNA sequence which is based upon the definition and algorithm in (19).
In this article, we describe a new database, TRedD, which stores the tandem repeats found in the human genome by the TRed software. The database is available online with an extremely easy to use interface. It contains graphical depictions of results using new and original GUI software. The results in this database have been compared to TRDB, and in some ways are similar, yet they differ in many reports as well. It is our hope that biologists will use this data to achieve further discoveries in the understanding of the human genome.
The remainder of the article is organized as follows. In ‘Preliminaries’ section, we review the underlying definition of tandem repeats, and the algorithm that is used to locate them. In ‘Database, homepage’ section, we discuss the database homepage, and in ‘The TRedD database’ section we describe the visualization of results. In ‘Current and future work’ section, we present an overview of our current work, and we conclude in ‘Conclusion’.
Preliminaries
Although it is possible to use the TRedD database as is, it would be beneficial to understand the underlying definition of approximate tandem repeats that is used by the TRed software. In this section, we give a summary of the definition and the concepts of the algorithm used in TRed.
Definition
The definition of tandem repeats over the ‘edit distance’ uses the model of ‘evolutive tandem repeats’ (20). The model assumes that each copy of the repeat, from left to right, is derived from the previous copy through zero or more mutations. Thus, each copy in the repeat is similar to its predecessor and successor copy.
The edit distance between two strings is defined as the minimum number of insertions, deletions and character replacements necessary to transform one string into another. Let denote the edit distance between two strings.
Definition 1A word r is a K-edit repeat if it can be partitioned into consecutive subwords,
,
, such that
, where
is some suffix of
and
is some prefix of
.
A K-edit repeat is a sequence of ‘evolving’ copies of a pattern such that there are at most K insertions, deletions and mismatches, overall, between all consecutive copies of the repeat. For example, the word r = caagctcagctccgct is a two-edit repeat.
In the output of the program, we display a tandem repeat as a multiple alignment of its copies, or ‘periods’. Each gap is represented by the hyphen -. If a period p of the repeat has a gap against its preceding period, but does not for the following period, then we write the period p twice. In order to show that it is the same period (except for insertions and deletions), we omit the indices on that line. For example, suppose the above repeat r was found at location 157, it is displayed as follows.
Example 1
Repeat of length 16 found at location 157 with two errors:
157 caagct 162
163 ca-gct 167
cagct
168 ccgct 172
Note that in Example 1 the second period (163–167) is included ‘twice’ in the alignment, once as it aligns with the previous period (157–162) and once to align it with the following period (168–172).
The algorithm
The algorithm that finds all ‘K-edit repeats’ in a sequence, given an integer K, is based upon the following interesting fact. For every sequence that is a K-edit repeat, it is possible to create a two-sequence alignment of the sequence ‘with a shift of itself’ with insertions, deletions and mismatches. The following two-sequence alignment represents the repeat shown in Example 1.
caagctca-gctccgct
caagctcagctccgct
This two-sequence alignment can be split appropriately to obtain the periods of the tandem repeat shown in Example 1. A modified version of the Smith–Waterman dynamic programming algorithm can be used to locate all such subsequences within a sequence. This is the basis of our algorithm, which includes several speedups based upon (21–24).
Our software also includes a heuristical postprocessor that combines overlapping repeats that are similar. For efficiency concerns, our program takes an integer K as input. It then reports repeats with at most K errors. The postprocessor is more flexible, since it is very fast, and if there are repeats that should be joined, it will ignore the original value of K and join the parts into one reported repeat.
The general rule that our postprocessor uses to determine whether to combine two repeats is as follows. Recall that each repeat can be represented by a two-sequence alignment. If the corresponding two-sequence alignment of two overlapping repeats align at a pair of identical indices, then they will be combined into a single repeat.
Database homepage
The database homepage, http://tandem.sci.brooklyn.cuny.edu, contains a menu for navigating with the following options: About, Run Program, View Database, References, Contact and Download.
The ‘Run Program’ link allows the user to run the TRed program in the browser (i.e. on our server). The user is given the option of either uploading a file or pasting a sequence into a text box. This will work on relatively small sequences, up to 2 MB long. For longer sequences, the user may obtain the source code of our software for free. We have already distributed the code to more than two dozen research groups worldwide.
Our TRed software is customizable—details about the meaning of the input parameters are included in the Appendix 1. When running the software on the web site, the default parameters will be used, which are as follows: MAX_ERRORS: 10, MIN_LENGTH: 20, MIN_RATING: 15, MIN_PERIOD: 1, MAX_PERIOD: 250, ERROR_VAL: 3, START_POS: 1.
The ‘About’ link allows the user to explore the underlying definition and the details of the algorithm. It also allows the user to read about the different ‘input’ parameters that the program can accept, and about the different views of the ‘output’ generated by TRed. The ‘References’ link gives a list of the articles published in relation to this project. The ‘Download’ link provides links to the plain text format of the repeat tables for the 24 chromosomes of the Homo sapiens. The user can download a local copy of each of these tables for further processing. We also provide an email address from which the source code of the program can be requested.
In the following section we discuss the ‘View Database’ link which allows the user to view the existing data in the database. Since it took about 20 h to run TRed on each chromosome of Homo sapiens (on a dedicated Quad Core 1.8 GHZ Intel Xeon CPU server), this will save our users much time and effort. In addition, we have implemented many features to ease the navigation and analysis of the output.
The TRedD database
Currently, the TRedD database contains the tandem repeats found in the 24 chromosomes of Homo sapiens, chromosomes 1–22, X and Y. These chromosome sequences were downloaded from: ftp://ftp.ensembl.org/pub/release-42/homo_sapiens_42_36d/data/fasta/dna/. When the user follows the ‘View Database’ link, a connection to the database is established, and a table of all chromosomes that have been processed is shown, see Table 1.
| Sequence . | Repeats Found . | Date . |
|---|---|---|
| Homo_Sapiens.dna.chromosome.1 | 91 814 View Table View Graph | 12/17/2008 |
| Homo_Sapiens.dna.chromosome.2 | 92 525 View Table View Graph | 12/19/2008 |
| Homo_Sapiens.dna.chromosome.3 | 69 829 View Table View Graph | 12/20/2008 |
| Homo_Sapiens.dna.chromosome.4 | 69 485 View Table View Graph | 1/22/2009 |
| Homo_Sapiens.dna.chromosome.5 | 65 195 View Table View Graph | 1/23/2009 |
| Homo_Sapiens.dna.chromosome.6 | 62 481 View Table View Graph | 1/24/2009 |
| Sequence . | Repeats Found . | Date . |
|---|---|---|
| Homo_Sapiens.dna.chromosome.1 | 91 814 View Table View Graph | 12/17/2008 |
| Homo_Sapiens.dna.chromosome.2 | 92 525 View Table View Graph | 12/19/2008 |
| Homo_Sapiens.dna.chromosome.3 | 69 829 View Table View Graph | 12/20/2008 |
| Homo_Sapiens.dna.chromosome.4 | 69 485 View Table View Graph | 1/22/2009 |
| Homo_Sapiens.dna.chromosome.5 | 65 195 View Table View Graph | 1/23/2009 |
| Homo_Sapiens.dna.chromosome.6 | 62 481 View Table View Graph | 1/24/2009 |
This table contains one row per chromosome of the Homo sapiens (1–22,X,Y).
| Sequence . | Repeats Found . | Date . |
|---|---|---|
| Homo_Sapiens.dna.chromosome.1 | 91 814 View Table View Graph | 12/17/2008 |
| Homo_Sapiens.dna.chromosome.2 | 92 525 View Table View Graph | 12/19/2008 |
| Homo_Sapiens.dna.chromosome.3 | 69 829 View Table View Graph | 12/20/2008 |
| Homo_Sapiens.dna.chromosome.4 | 69 485 View Table View Graph | 1/22/2009 |
| Homo_Sapiens.dna.chromosome.5 | 65 195 View Table View Graph | 1/23/2009 |
| Homo_Sapiens.dna.chromosome.6 | 62 481 View Table View Graph | 1/24/2009 |
| Sequence . | Repeats Found . | Date . |
|---|---|---|
| Homo_Sapiens.dna.chromosome.1 | 91 814 View Table View Graph | 12/17/2008 |
| Homo_Sapiens.dna.chromosome.2 | 92 525 View Table View Graph | 12/19/2008 |
| Homo_Sapiens.dna.chromosome.3 | 69 829 View Table View Graph | 12/20/2008 |
| Homo_Sapiens.dna.chromosome.4 | 69 485 View Table View Graph | 1/22/2009 |
| Homo_Sapiens.dna.chromosome.5 | 65 195 View Table View Graph | 1/23/2009 |
| Homo_Sapiens.dna.chromosome.6 | 62 481 View Table View Graph | 1/24/2009 |
This table contains one row per chromosome of the Homo sapiens (1–22,X,Y).
This table has columns for the sequence name, the number of repeats found and the date the program was run. In the ‘Repeats Found’ column, the number of repeats found in the chromosome is displayed, as well as two links for viewing the results, ‘View Table’ and ‘View Graph’. Since this is the most important aspect of the database for the novice user, we devote the following two subsections to the viewing of results.
Table view
If the user selects ‘View Table’ in the ‘Repeats Found’ column (see Table 1), a table of the results for that specific chromosome is displayed. See Table 2 for the first few lines of the table of repeats for chromosome 1 of Homo sapiens. The table contains one line per tandem repeat found, with the following data on each repeat: Alignment, Start, End, Length, Period, Repetitions, Errors and Percent Match. The Alignment column is a link that allows the user to view the actual multiple alignment of the copies of the repeat. See Table 3 for the alignment that appears when the user clicks on the second line in Table 2. In ‘Definition’ Section, we described the details of how the alignment is generated.
The table view of the repeats shows details about the repeats found in a chromosome
| Homo Sapiens Chromosome 1 . | |||||||
|---|---|---|---|---|---|---|---|
| Alignment . | Start . | End . | Length . | Period . | Repetitions . | Errors . | % Match . |
| View | 1 | 468 | 468 | 6.1 | 77.2 | 20 | 95.75 |
| View | 621 | 860 | 240 | 74.8 | 3.2 | 7 | 95.83 |
| View | 9169 | 9308 | 140 | 70.0 | 2.0 | 5 | 92.96 |
| View | 20 718 | 20 755 | 38 | 1.9 | 20.0 | 4 | 89.19 |
| View | 20 726 | 20 785 | 60 | 13.0 | 4.6 | 6 | 87.50 |
| Homo Sapiens Chromosome 1 . | |||||||
|---|---|---|---|---|---|---|---|
| Alignment . | Start . | End . | Length . | Period . | Repetitions . | Errors . | % Match . |
| View | 1 | 468 | 468 | 6.1 | 77.2 | 20 | 95.75 |
| View | 621 | 860 | 240 | 74.8 | 3.2 | 7 | 95.83 |
| View | 9169 | 9308 | 140 | 70.0 | 2.0 | 5 | 92.96 |
| View | 20 718 | 20 755 | 38 | 1.9 | 20.0 | 4 | 89.19 |
| View | 20 726 | 20 785 | 60 | 13.0 | 4.6 | 6 | 87.50 |
The first five repeats found in chromosome 1 of Homo sapien are shown in this table
The table view of the repeats shows details about the repeats found in a chromosome
| Homo Sapiens Chromosome 1 . | |||||||
|---|---|---|---|---|---|---|---|
| Alignment . | Start . | End . | Length . | Period . | Repetitions . | Errors . | % Match . |
| View | 1 | 468 | 468 | 6.1 | 77.2 | 20 | 95.75 |
| View | 621 | 860 | 240 | 74.8 | 3.2 | 7 | 95.83 |
| View | 9169 | 9308 | 140 | 70.0 | 2.0 | 5 | 92.96 |
| View | 20 718 | 20 755 | 38 | 1.9 | 20.0 | 4 | 89.19 |
| View | 20 726 | 20 785 | 60 | 13.0 | 4.6 | 6 | 87.50 |
| Homo Sapiens Chromosome 1 . | |||||||
|---|---|---|---|---|---|---|---|
| Alignment . | Start . | End . | Length . | Period . | Repetitions . | Errors . | % Match . |
| View | 1 | 468 | 468 | 6.1 | 77.2 | 20 | 95.75 |
| View | 621 | 860 | 240 | 74.8 | 3.2 | 7 | 95.83 |
| View | 9169 | 9308 | 140 | 70.0 | 2.0 | 5 | 92.96 |
| View | 20 718 | 20 755 | 38 | 1.9 | 20.0 | 4 | 89.19 |
| View | 20 726 | 20 785 | 60 | 13.0 | 4.6 | 6 | 87.50 |
The first five repeats found in chromosome 1 of Homo sapien are shown in this table
The multiple alignment of the periods of the second repeat found in chromosome 1 of Homo sapiens, occurring at locations 621–860
| 621 | GGCGCAGGCGCAGAGAGGCGCGCCGCGCCGGCGCAGGCGC–AGACACATGCTAGCGCGTC–GGGGTGGAGGCGT | 692 |
| 693 | GGCGCAGGCGCAGAGAGGCGCGCCGCGCCGGCGCAGGCGCAGAGACACATGCTACCGCGTCCAGGGGTGGAGGCGT | 768 |
| 769 | GGCGCAGGCGCAGAGAGGCGCACCGCGCCGGCGCAGGCGCAGAGACACATGCTAGCGCGTCCAGGGGTGGAGGCGT | 844 |
| 845 | GGCGCAGGCGCAGAGA | 860 |
| 621 | GGCGCAGGCGCAGAGAGGCGCGCCGCGCCGGCGCAGGCGC–AGACACATGCTAGCGCGTC–GGGGTGGAGGCGT | 692 |
| 693 | GGCGCAGGCGCAGAGAGGCGCGCCGCGCCGGCGCAGGCGCAGAGACACATGCTACCGCGTCCAGGGGTGGAGGCGT | 768 |
| 769 | GGCGCAGGCGCAGAGAGGCGCACCGCGCCGGCGCAGGCGCAGAGACACATGCTAGCGCGTCCAGGGGTGGAGGCGT | 844 |
| 845 | GGCGCAGGCGCAGAGA | 860 |
This corresponds to row 2 in Table 2.
The multiple alignment of the periods of the second repeat found in chromosome 1 of Homo sapiens, occurring at locations 621–860
| 621 | GGCGCAGGCGCAGAGAGGCGCGCCGCGCCGGCGCAGGCGC–AGACACATGCTAGCGCGTC–GGGGTGGAGGCGT | 692 |
| 693 | GGCGCAGGCGCAGAGAGGCGCGCCGCGCCGGCGCAGGCGCAGAGACACATGCTACCGCGTCCAGGGGTGGAGGCGT | 768 |
| 769 | GGCGCAGGCGCAGAGAGGCGCACCGCGCCGGCGCAGGCGCAGAGACACATGCTAGCGCGTCCAGGGGTGGAGGCGT | 844 |
| 845 | GGCGCAGGCGCAGAGA | 860 |
| 621 | GGCGCAGGCGCAGAGAGGCGCGCCGCGCCGGCGCAGGCGC–AGACACATGCTAGCGCGTC–GGGGTGGAGGCGT | 692 |
| 693 | GGCGCAGGCGCAGAGAGGCGCGCCGCGCCGGCGCAGGCGCAGAGACACATGCTACCGCGTCCAGGGGTGGAGGCGT | 768 |
| 769 | GGCGCAGGCGCAGAGAGGCGCACCGCGCCGGCGCAGGCGCAGAGACACATGCTAGCGCGTCCAGGGGTGGAGGCGT | 844 |
| 845 | GGCGCAGGCGCAGAGA | 860 |
This corresponds to row 2 in Table 2.
Start and End show the loci in the chromosome of the start and end position of the tandem repeat. The length is the length of the repeat as its number of bases (end-start + 1). Since the period lengths of a given repeat are variable due to insertions and deletions, in the Period column we put the average period length. The Repetitions column tells the number of copies of the period in the tandem repeat, e.g. caggcaggcaggcag will have 3.75 copies. This corresponds to the number of rows in the multiple alignment. The Errors column tells the sum of the edit operations (insertions, deletions and mismatches) between consecutive periods of the repeat.
The table is paginated, and 100 repeats are shown per page. It is possible to sort each page by any one of the columns, in ascending or descending order, by clicking on the arrows in the column heading. Furthermore, it is possible to filter the output by one or more of several criteria. Suppose a user is interested in viewing long repeats, or repeats with large period size. Since there are so many repeats, sorting each table will be too cumbersome. We have therefore provided querying capabilities using mySQL queries.
To create a query, click the ‘Filter’ link immediately above the table. A query form will appear on the page, with the following fields: Start Location, End Location, Length, Errors, Minimum Period Size and Percent Match. The user can enter any starting and ending location in text boxes. This facilitates the search for repeats within known genes. The rest of the fields have pull-down menus for the user to choose from. These menus are dynamic, for e.g. the Length menu will range from the shortest repeat to the longest repeat found in this specific chromosome. The user has to simply choose values for the fields, click Submit, and only those repeats that satisfy the criteria will show in the table below. To close the filter, click again on the Filter link. This query feature is extremely useful in analyzing the myriad of output that is included in the database.
Graphical view using TandemGraph
Most genomes have high content of tandem repeats, and the Homo sapiens is no exception. In the sequence of chromosome 1, TRedD contains 91 814 repeats. In the table view (described in the previous section), these repeats are displayed to the end user in tables, one line per tandem repeat, 100 lines per table. This yields 919 pages for chromosome 1 alone. In order for biologists to be able to analyze this data, we felt that it must be presented in a clear graphical visualization, allowing both a high-level overview and variant levels of detail. To this end, we have developed a new software tool called ‘TandemGraph’ to graphically depict the tandem repeats in a sequence (25). TandemGraph allows one to view the entire set of tandem repeats in a chromosome in a single image, and then to continuously zoom in to see further details.
The idea of the representation used in TandemGraph is largely based upon the model of the pygram (or pyramid diagram) (26), which uses overlaid triangles, in a similar manner to an earlier design called the ‘landscape’ (27). Our model uses overlaid outlined colored triangles to represent the tandem repeats (see Figure 1). Each triangle represents one tandem repeat; thus, each triangle in the graph corresponds to one row in the table view. Given a sequence S of length n, and a list of the substrings of S that are tandem repeats, a representation is a two-dimensional graph, where the x-axis is labeled with the actual sequence, and triangles are drawn in the matrix above, with the height of each triangle representing the length of the repeat. The left x-coordinate of each triangle represents the first nucleotide of the repeat sequence, while the right x-coordinate represents the end of the repeat. The triangles are outlined, therefore all overlapping repeats are clearly visualized.
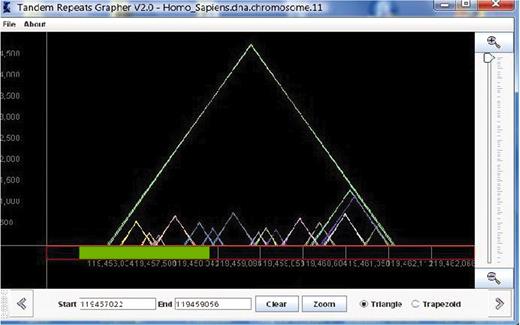
This view of TandemGraph shows the repeats that occur in a segment of chromosome 11 of the Homo sapiens. Each triangle represents a tandem repeat. Below the graph, the green bar represents a new zooming segment, and the text boxes allow entry of actual indexes for zooming.
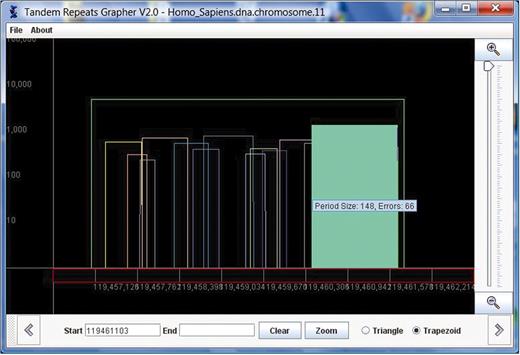
Information about other attributes, such as period size and percent error, appear in a triangle as the user mouses over the triangle. In addition, as the mouse is placed in a triangle, the triangle gets filled in, to clarify which of the overlapping triangles is selected. Once a triangle is selected, the user can click on it to view the multialignment of the actual repeat. This corresponds exactly to the user clicking ‘View Alignment’ in the specific row of the table. In Figure 2, we show the same view as in Figure 1 with a triangle selected.
The same view of chromosome 11 as shown in Figure 1 is shown here. In this figure, a triangle has been selected, and the multiple alignment of this repeat is displayed in a pop-up window.
Zooming features: the highest level view represents an entire chromosome. For this level the graph generally degenerates to a column graph, each column representing a repeat, with the height of the line representing the repeat's length. If there is more than one repeat located at the same (or close) location, the column will appear as a multicolored line, the bottom part representing the shortest repeat, the piece above another color representing the next longer repeat and so on.
Zooming has been implemented in several different user-friendly ways. The slider at the right provides a continuous zoom, with zoom-out and zoom-in buttons on top and bottom. The red rectangle on the bottom allows the user to drag a range of the chromosome to zoom, while the text boxes underneath the rectangle allow the user to enter actual start and end locations in the chromosome. All three of these zooming features are fully integrated, so that the actual indices appear in the start and end box as the user drags through a range.
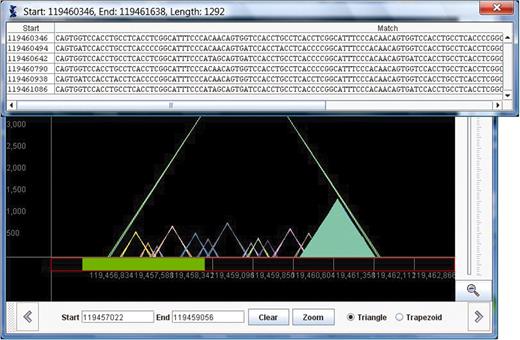
Log-graph: in some chromosomes there are repeats that are extremely long, possibly spanning over 100 000 bases. These long repeats cause the STR (which are much more common) to be barely visible as their heights scale to close to zero. In situations where data covers a large range of values it is common to present the data on a logarithmic scale. Thus, the y-axis is labeled with powers of 10 (10, 100, 1000, etc.). A repeat with length has height
. Using the log-scale, a triangle that represents a repeat that is a substring of another repeat will not necessarily fit entirely inside its superstring's triangle. Therefore, we represent repeats as trapezoids. The left and right x values are the same as described above for the triangles, and the height of the trapezoid is
where
represents the repeat's actual length. TandemGraph includes radio buttons to allow the user to switch the graph from triangles and linear heights to trapezoids and log-scale heights. In Figure 3 , we show the same area in chromosome 11 that is shown in both Figures 1 and 2, with the trapezoid button selected.
We have run TandemGraph on all 24 chromosomes of Homo sapiens (1–22,X,Y) and the results are excellent. TandemGraph provides a GUI interface to huge amounts of data, previously available as text only. We have fully integrated the TandemGraph tool with the TRedD database. Thus, when the user chooses ‘View Graph’, the TandemGraph application opens, automatically connects to the TRedD database and downloads the information about the repeats. There is a menu of all of the chromosomes in the human genome in TandemGraph, so that the user can switch to a different chromosome without returning to the browser.
Note: In order to run TandemGraph directly from the browser, it is necessary to have java installed on your computer. Java is available as a free download from Sun Microsystems at http://java.com/en/download/. It is also preferable to use Firefox to open the java program. Using Internet Explorer, it is necessary to save and rename the executable with a .jar filename extension.
Current and future work
We have several plans of enhancements to the TRedD database that are under way. In this section, we discuss two of the projects that we are currently working on: comparing our results with other tandem repeats data, and merging our data with existing annotation.
Evaluation of the repeats found in TRedD
There are two different general approaches to defining an approximate tandem repeat. The first is a consensus-type repeat, that is, there is some string called a consensus, that is similar to all copies of the repeat. Note that it is possible that the consensus string does not appear as an exact copy in the repeat. We say that a repeat has K errors, if the pairwise sum of the errors between each copy and the consensus is K. Benson et al. in TRDB (11) follow the consensus approach.
Our approach is different, in that we consider evolutive repeats, where we relate each copy to the preceding and following copy. We count the errors between adjacent copies, and there is not necessarily any agreement over all of the copies. The assumption here is that each copy is derived from a neighboring copy, possibly with mutations.
Following is an interesting observation relating the two different definitions.
Observation 1Every consensus type repeat with K errors, is also an evolutive repeat with no more than 2K errors.
This observation can be proven by considering the changes necessary to convert a copy into the consensus, and then converting the consensus into the following copy. We point out that this observation does not work vice versa.
Following this observation, we see that any program that finds evolutive tandem repeats should find consensus-type repeats as well. This has been confirmed to some extent by tests that we have been running to compare our results with the results of TRDB. Many of the repeats found in TRDB are found almost identically in TRedD. In addition, TRedD should contain repeats that are inherently evolutive; those repeats are not found by a consensus-repeat program. It is stated in the literature that evolutive tandem repeats occur in biological sequences (20). We are in the midst of analyzing the additional results of our program to determine what kind and how many evolutive tandem repeats actually occur in the human genome. In chromosome 1, our preliminary tests have revealed that 36% of the repeats found in TRedD have no overlapping repeats in the output of TRDB. Following we give a simple example of a repeat that occurs in chromosome 1 that is inherently evolutive.
Example of evolutive-type repeat which does not have a consensus
The period begins as TGTA, changes to TATA, TATG, TAT, and then TT.
227807473 TGTA 227807476
227807477 TGTA 227807480
227807481 TATA 227807484
227807485 TATA 227807488
227807489 TATA 227807492
227807493 TATG 227807496
227807497 TAT- 227807499
TAT
227807500 T-T 227807501
TT
227807502 TT 227807503
227807504 TT 227807505
227807506 TT 227807507
227807508 T 227807508
Errors: 4 Percent Matching: 88.24%
Following is another very interesting example that we noticed during evaluation. In TRDB, four different repeats are reported, beginning and ending at the same locations as the following repeat. Our program reports this as one repeat, with a changing period size, averaging 24.2. This different view of (perhaps) the same repeat illustrates the importance of using different definitions and software for locating tandem repeats in the human genome.
TRDB output:
Start End Period Size
110832 110998 11
110832 110998 9
110832 110998 20
110832 110998 26
TRed output:
Start: 110832 End: 111001 Period Size: 24.2
110832 TATATATTATATATCTATTA 110851
110852 TATATAATATATATCTATTA 110871
TATAT-A-ATAT–-ATATCTATTA
110872 CATATTATATATTGTATATCTATTA 110896
CATAT-TAT-ATAT-TGTATATCTATTA
110897 CATATATATTATATATGTAT-TATAT-A 110922
CAT-ATATATTATATATGTATTATATA
110923 TATTATATATTATATATGTATTATATA 110949
110950 TATTATATATTATATATCTATTATATA 110976
TATTATATATTATATATCTATTATAT-A
110977 TA-TA-ATATTATATAT-TA-TATATCA 111000
111001 T 111001
Relating repeats to known genes and diseases
There are numerous popular biological databases that include information about the human genome and the genes occurring in the human genome. It is important that our data be understood in the context of this existing information, in a setting that is familiar to researchers in biology. In order to integrate our data with other known genomic features that are interesting to biologists, we are working on joining our data with a well-known Genome Browser. Our first attempt is through the UCSC Genome Browser (28) (http://genome.ucsc.edu/cgi-bin/hgCustom?hgsid=148664807), due to its popularity among biologists. We are using the genomic annotations, i.e. standard tracks, and the configuration for adding extra information called ‘custom annotation tracks’.
We have begun parsing our data into GFF format in order to be able to upload it to the UCSC browser as a custom track. In Figure 4, we show an example of the UCSC genome browser for gene TNFSF9 from human chromosome 19, which extends from start location 6 482 010 to end location 6 486 939. We chose this particular range of chromosome 19, since there are known disease genes in this range (18). We have turned off most of the tracks that come with UCSC's browser, and kept only the genes, repeat masker and simple repeat tracks. Our custom track is red and it is labeled TRED.
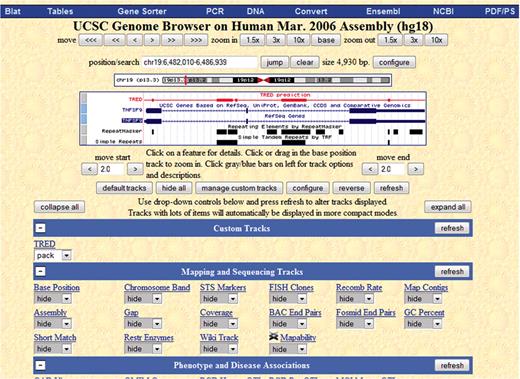
This figure is the view of the UCSC genome browser of gene TNFSF9 from human chromosome 19. The custom track is the red one, and it is labeled Tred.
We have checked eight genes manually, and it seems that our results ‘agree’ with the repeat masker and simple repeat on a larger scale but are not exactly the same (which is expected). In Figure 4, we chose an example that shows that our repeats are similar to known repeat prediction but are still different enough that they warrant further investigation.
Currently, we are in the midst of:
Adding repeat results from all of the chromosomes as custom tracks. This will integrate our results with the genomic features available in UCSC's genome browser.
Adding all repeat results from other repeats databases, such as TRDB. This will facilitate the comparison of our results with results from other repeat finding software.
Evaluating pros and cons between the UCSC genome browser and other browsers such as JBrowse (http://gmod.org/wiki/JBrowse).
Implementing two-way search between repeat elements and annotated genomic features.
Conclusion
We have created a database of tandem repeats in the human genome based upon a new and innovative definition of evolutive tandem repeats. We have also developed a tool to graphically depict the repeats occurring in a sequence which will greatly facilitate analysis of results. This tool can be used as well with other repeat-finding software, and we will distribute it freely.
Some questions that may be asked about evolutive tandem repeats concern the frequency and the levels of mutational difference between adjacent copies within a repeat. Non-uniform patterns of difference may suggest that the mutation process favors a restricted range of copy-to-copy similarity. It is our hope that the scientific community will use our database to gain new insights into tandem repeats in DNA, and we invite users to give feedback and suggestions.
Funding
National Science Foundation (grant number DB&I 0542751) Professional Staff Congress-City University of New York Research Award Program (grant number 62280-0040i). Funding for the Open Access charge: National Science Foundation Grant.
Conflict of interest statement. None declared.
References
Appendix 1:
Input parameters for the TRed software
MAX_ERRORS: the maximum allowed number of errors in a repeat. Higher values make the program run much slower, lowering it will make the program run much faster.
MIN_LENGTH: the minimum length of reported repeats.
MIN_RATING: the rating is an approximation of the number of matches in the repeat minus the number of errors in the repeat multiplied by ERROR_VAL. In other words, each match adds 1 to the rating, while each error subtracts from the rating an amount equal to ERROR_VAL. Thus, in order for a repeat to be reported it needs ERROR_VAL matches for each error, plus an additional MIN_RATING matches. Aside from influencing the amount of output the program gives, this value has a negligible effect on the speed of the program. Default value is 15.
MIN_PERIOD: the period of an evolutive tandem repeat may change throughout the repeat. Thus, only repeats whose periods are larger than or equal to this value throughout the repeat are guaranteed to be detected.
MAX_PERIOD: the maximum period length. Repeats with periods up to the size of MAX_PERIOD will be detected. ERROR_VAL: this is how much an error counts against the rating. See MIN_RATING for details.
START_POS: the index of the first character of your input string. Default value is 1.
UNKNOWN: the character in the input sequence that represents an unknown base. Default character is ‘N’.